9指数与指数幂的运算

1.教学根式的概念及运算：

① 复习实例蕴含的概念：,就叫4的平方根；，3就叫27的立方根.

探究：,就叫做的？次方根, 依此类推,若,那么叫做的次方根. 

② 定义n次方根：一般地，若,那么叫做的次方根.(  th  root ),其中,

简记：.    例如：，则

③ 讨论：当n为奇数时, n次方根情况如何？, 例如: ,,  

记：

当n为偶数时，正数的n次方根情况？ 例如: ,的4次方根就是, 记：

强调：负数没有偶次方根,0的任何次方根都是0, 即. 

④ 练习：,则的4次方根为     ； , 则的3次方根为      .

⑤ 定义根式：像的式子就叫做根式（radical）, 这里n叫做根指数（radical exponent）,  a叫做被开方数（radicand）.

⑥ 计算、、 → 探究： 、的意义及结果？ （特殊到一般）

结论：. 当是奇数时，；当是偶数时，

2、例题讲解求下列各式的值

               

3.课堂练习

1. 计算或化简：； 

2、求值化简：  ；   ；  ；  （）

2、分数指数幂

① 引例：a>0时，  →         ； 

  →      .

① 定义分数指数幂：

规定；

③ 练习：A.将下列根式写成分数指数幂形式：

；；

3.求值：

（1）            (2)　         （3）      

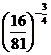 (4)        （5） 

课堂练习求下列各式的值：

 ;    ;   ； ； ； ； 

④ 讨论：0的正分数指数幂？ 0的负分数指数幂？⑤ 指出：规定了分数指数幂的意义后，指数的概念就从整数指数推广到了有理数指数，那么整数指数幂的运算性质也同样可以推广到有理数指数幂．

3.指数幂的运算性质：

·；  ； ．

4.用根式的形式表示下列各式（）：

       ；          ；           ；           。

5.用分数指数幂的形式表示下列各式（其中a＞0）

=             =             =           

针对训练：

1．用分数指数幂表示下列各式：

（1）；         （2）；        （3）；

（4）；   （5）；     （6）。

2．求下列各式的值：

（1）；          （2）；            （3）；         

（4）；       （5）；      （6）

3、求值:;    ;     ;      

4、化简：；

5、计算

6．计算下列各式（式中字母都是正数）

（1）；         （2）

（2）（后边括号里该成减号）

例1．（P52，例4）计算下列各式（式中字母都是正数）

（1）

（2）

例2．（P52例5）计算下列各式

（1）

（2）＞0）