数学（文科）

第Ⅰ卷

一、选择题（本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）

1、设复数的虚部记作，已知为虚数单位，则（     ）

A．-3       B．3       C．-2        D．2

2、已知集合，则

A．     B．     C．     D．     

3、已知数据，由此求得线性回归方程，则“满足线性回归方程”是“”的（    ）

A．充分不必要条件     B．必要不充分条件     

C．充要条件           D．既不充分也不必要条件     

4、设函数是定义在R上的奇函数，当时，，则（   ）

A．     B．     C．     D．     

5、如图，网格纸是由边长为x的小正方形组成，某几何体的三视图如图中粗线所示，已知该几何体的体积为128，则

 A．1     B．2     C．3     D．     

6、已知，若，则下列结论中，不可能成立的是

A．     B．     C．     D．     

7、执行如图所示的程序框图，则输出的结果是

A．     B．    

C．     D．     

8、已知向量，且，

则等于

A．3     B．    

C．     D．     

9、已知变量满足不等式组表示的区域为D，

B、C为区域D内的任意两点，设的夹角为，则的****值是（    ）

A．     B．     C．     D．     

10、已知的导函数，若记在求导的结果为，以此类推，则（  ）

A．2        B．0        C．-1       D．1

11、某校鲁班学习小组利用课余时间模拟制作奥运圣火采集器，已知他们制作采集器的抛物面的轴切线为经过定点的抛物线，则该抛物线的焦点与双曲线在一三象限内的渐近线  

的距离为（    ）

A．     B．或     C．     D．或     

12、已知函数，函数，若方程有两个不同的实根，则的取值范围为（    ）

A．     B．     C．     D．     

第Ⅱ卷

二、填空题：本大题共5小题，每小题5分，共25分，把答案填在答题卷的横线上。.

14、2014巴西足球世界杯最终以德国队高举大力神杯而落幕，****认为：“中国的孩子既没时间也没场地踢球，现在急需足球这样的全民健身运动，当从民族的高度、战略的高度发展足球”，以下是某新闻媒体进行的网上调查，所有参与调查的人中，持“支持”、“中立”和“不支持”态度的人数如下表所示:

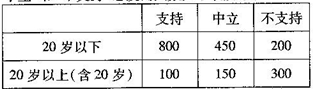
在所有参与调查的人中，用分层抽样的方法抽取n个人，已知从“支持”态度的人中抽取了45人，则              

14、与圆相交所得的弦长为2，且与直线垂直的直线方程是            

15、已知是各项均为正数的等比数列，且，则          

16、定义函数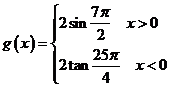，设，其中，若恒成立，则实数m的取值范围为           

三、解答题：本大题共6小题，满分75分，解答应写出文字说明、证明过程或演算步骤

17、（本小题满分12分）

  保持口腔卫生不仅对牙齿健康有好处，对预防早老性痴呆症（阿尔茨海默氏症）也是一个十分重要的因素，某市医疗工作人员对某社区人鱼进行了刷牙次数的统计，随机抽取了40人作为样本，得到这40人每月刷牙的次数，根据此数据得到频率分布表和频率分布直方图如下：

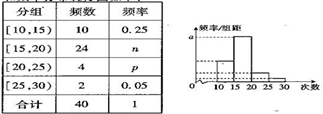
（1）求互表中p即图中a的值；

 （2）若该社区有240人，试估计该社区每月刷牙次数在区间内的人数；

 （3）在所取样本中，从每月刷牙的次数不少于20次的人员中任选2人，求至多一人每月刷牙次数在区间内的概率。

18、（本小题满分12分）

   在中，角所对边的边长分别为，其中，的面积为15，其外接圆的半径。

（1）求的值；

 （2）求的周长。

19、（本小题满分12分）

  如图，在三棱柱中，侧棱底面，是等边三角形，D为AC的中点，求证：

（1）平面平面；

 （2）平面

20、（本小题满分12分）

  已知函数，且在上是增函数，

（1）求实数的取值范围；

 （2）求在区间上的最小值。

21、（本小题满分14分）

  已知椭圆，其焦距为4，双曲线，的离心率互为倒数。

（1）求椭圆的标准方程；

 （2）过椭圆的右顶点作直线交抛物线于两点，过原点与两点的直线分别与椭圆相较于点，证明为定值。

请考生在第（22）、（23）（24）三体中任选一题作答，如果多做，则按所做的第一题记分，作答时用2B铅笔在答题卡上把所选题目的题号涂黑，把答案填在答题卡上．

22、（本小题满分10分）

  如图，已知PE为圆的切线，切点为E，割线PBA交于A、B两点，C为AE上一点，

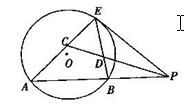且CPE=CPA

（1）已知DE=3，PE=6，PB=4，求的值；

 （2）求证：.

23、（本小题满分10分）

  在极坐标系中，已知曲线为过定点且与直线平行的直线，A、B分别为曲线C和直线上的动点。

（1）求曲线C和直线分别化为直角坐标系下的方程；

 （2）求的最小值。

24、（本小题满分10分）

  已知函数

（1）当时，求函数的****值；

 （2）解关于x的不等式。