1. 线性规划及其相关概念

(1) 目标函数:欲达到****值或最小值所涉及的变量x,y的解析式称为目标函数.关于x,y的一次目标函数称为线性目标函数.

(2) 约束条件:由x,y的不等式(或方程)组成的不等式组称为x,y的约束条件.关于x,y的一次不等式或方程组成的不等式组称为x,y的线性约束条件.

(3) 可行解:满足线性约束条件的解(x,y)称为可行解.

(4) 可行域:所有可行解组成的集合称为可行域.

(5) 最优解:使目标函数取得****值或最小值的可行解称为最优解.

(6) 求线性目标函数在线性约束条件下的****值或最小值问题称为线性规划问题.

2. 解线性规划问题的步骤

(1) 画,即画出线性约束条件所表示的可行域;

(2) 移,即在线性目标函数所表示的一组平行线中,利用平移的方法找出与可行域有公共点且纵截距****或最小的直线;

(3) 求,即通过解方程组求最优解;

(4) 答,即给出答案.

1. (必修5P77练习1改编)若点(-2,t)在直线2x-3y+6=0的上方,则t的取值范围是　　　　.

[答案]

[解析]因为点(-2,t)在直线2x-3y+6=0的上方,所以2×(-2)-3t+6<0,解得t>.

2. (必修5P78例1改编)若变量x,y满足约束条件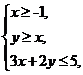则z=2x+y的****值为　　　　.

[答案]3

[解析]作出可行域如图中阴影部分所示,可得直线y=x 与3x+2y=5的交点为最优解点,即为(1,1).当x=1,y=1时,z_max=3.

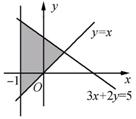
(第2题)　　

3. (必修5P78例1改编)已知实数对(x,y)满足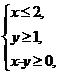，则2x+y取最小值时的实数对是　　　　.

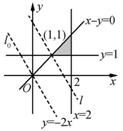
(第3题)

[答案](1,1)

[解析]作出可行域如图中阴影部分所示,令z=2x+y,y=-2x+z,作直线y=-2x,作与l₀平行的直线l,则直线l经过点(1,1)时,(2x+y)_min=3.

4. (必修5P80练习1改编)若变量x,y满足约束条件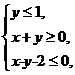则z=x-2y的****值为　　　　.

[答案]3

[解析]作出可行域如图中阴影部分所示,z=x-2yÞy=x-z,由图可知,当直线经过点A(1,-1)时,z取得****值3.

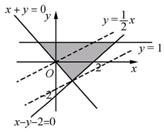
(第4题)