8．D　本题考查v ­ t 图象．由于两质点的速度均为正，因此两质点的运动方向相同，A错误；由于t＝3 s时两质点相遇，根据图象所围的面积可知，t＝0时刻，两质点不在同一位置，B错误；由题意可知，t＝3 s时，甲质点的速度大小为v＝10 m/s，t＝3 s时第二次相遇，则t＝2 s时，两质点相距Δx＝2(1)×6×1 m＝3 m，C错误；根据比例关系可知，t＝2 s时，甲、乙的速度均为3(20) m/s，则乙做匀减速运动的加速度大小a＝1(－4) m/s²＝3(8) m/s²，则乙在t＝0时刻的速度大小为v＝4 m/s＋3(8)×3 m/s＝12 m/s，D正确．

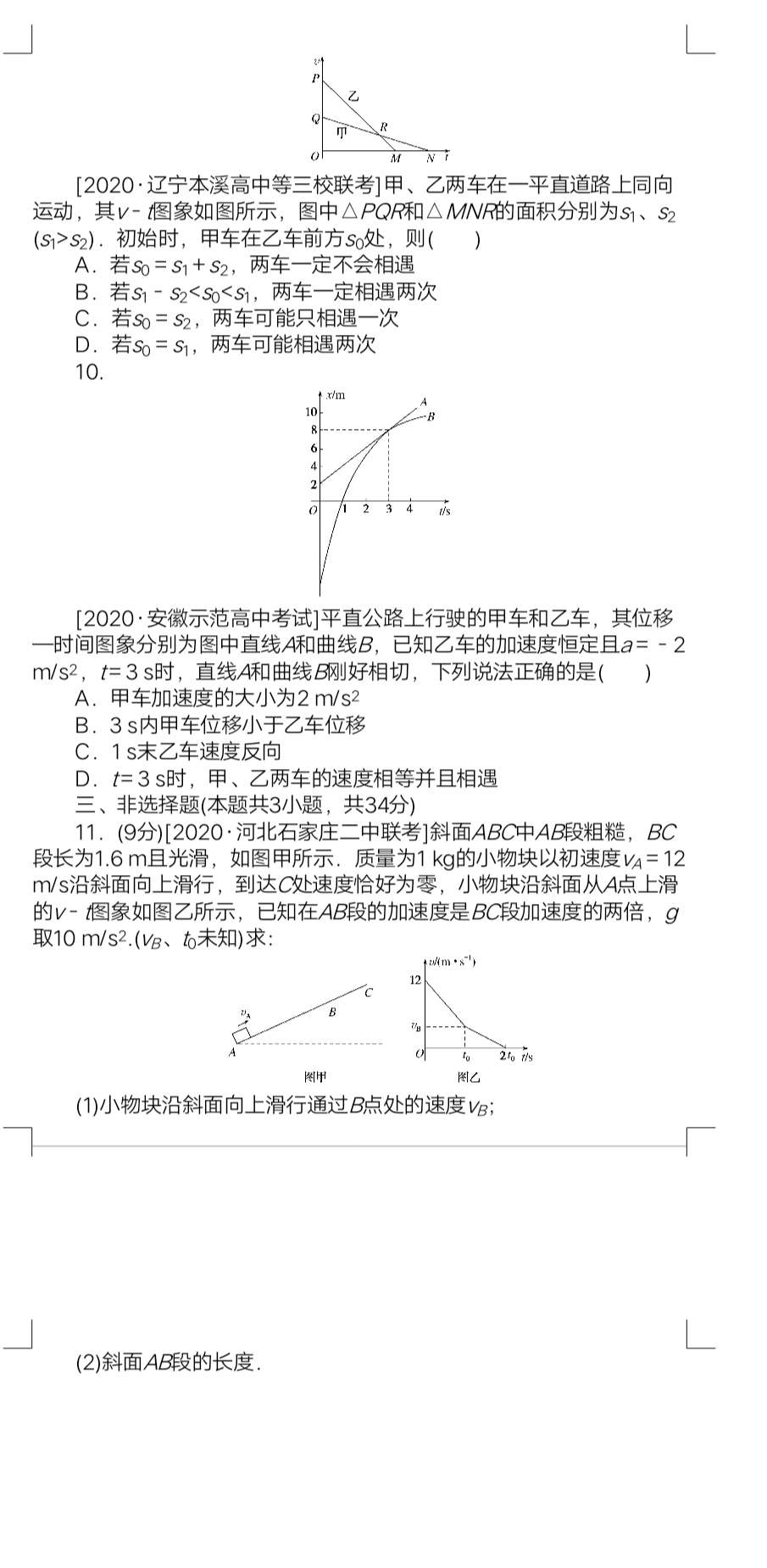
9．ABC　若s₀＝s₁＋s₂，则有s₀>s₁，说明两车速度相同时乙还没有追上甲，不能相遇，速度相同后甲的速度比乙速度大，所以两车一定不会相遇，故A正确；若s₀<s₁，两车在速度相同前就相遇一次，之后，若s₁－s₂<s₀，两车会发生第二次相遇，故B正确；若s₀＝s₂，则s₀<s₁，两车在速度相同前相遇一次，故C正确；若s₀＝s₁，两车只在速度相同时相遇一次，故D错误．

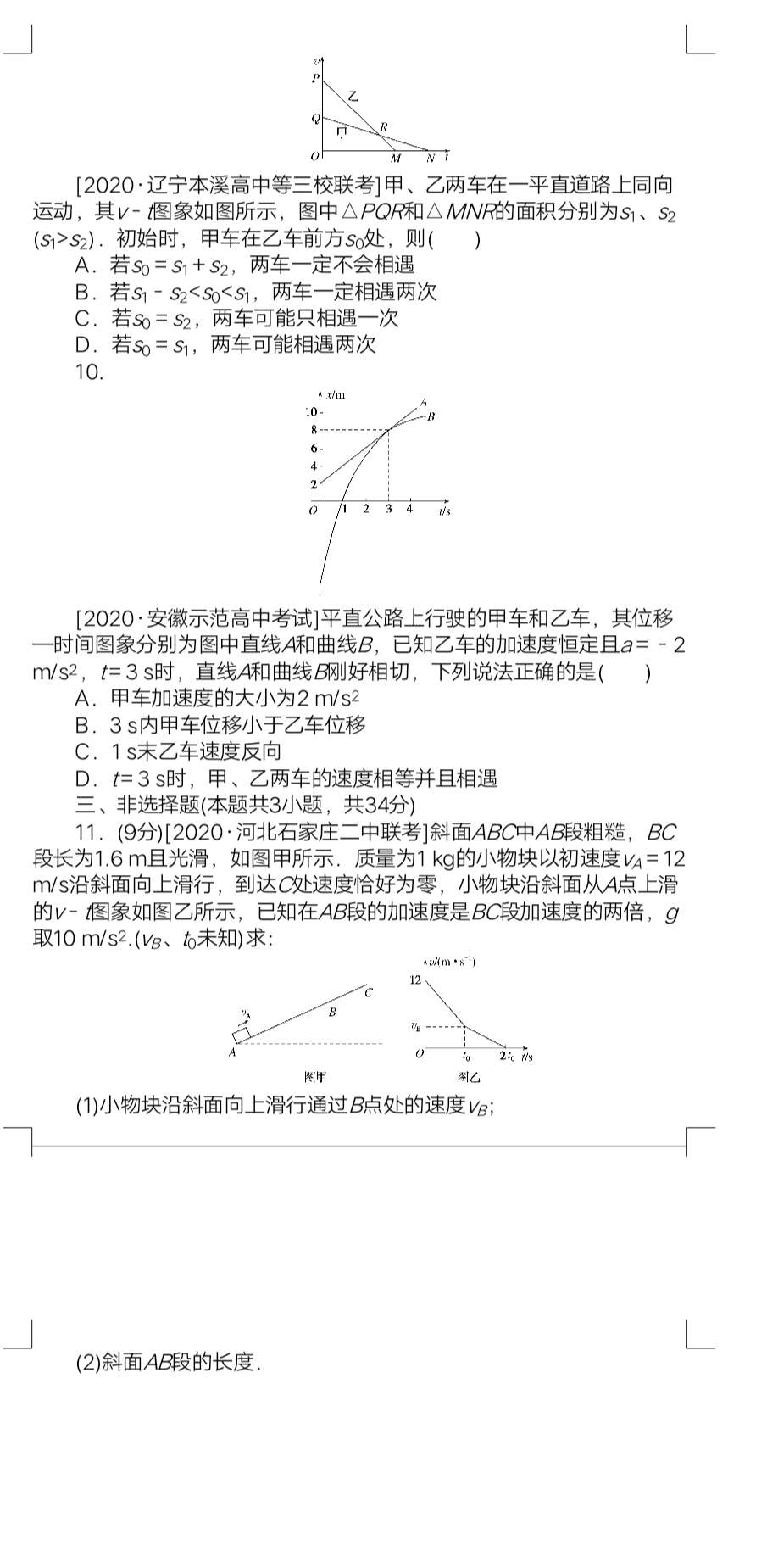
10．BD　甲车做匀速直线运动，其加速度的大小为零，选项A错误；根据位移—时间图象的斜率表示速度，可知1 s末乙车的速度仍是正值，选项C错误；根据位移—时间图象的斜率表示速度，t＝3 s时，直线A和曲线B刚好相切，可知t＝3 s时，甲、乙两车的速度相等并相遇，选项D正确；根据位移—时间图象的斜率表示速度，可知t＝3 s时乙车的速度v_乙＝2 m/s，由v_乙＝v₀＋at可得，v₀＝8 m/s,3 s内甲车从x＝2 m运动到x＝8 m，位移为6 m，乙车位移s＝v₀t＋2(1)at²＝8×3 m＋2(1)×(－2)×3² m＝15 m，所以3 s内甲车位移小于乙车位移，选项B正确．

11．答案：(1)4 m/s　(2)6.4 m

解析：(1)由v－t图象可知，小物块沿斜面向上滑行的初速度v_A＝12 m/s，由a_AB＝2a_BC可得，t0(vA－vB)＝2t0(vB)，解得v_B＝4 m/s.

(2)在上滑过程对AB段有vB(2)－vA(2)＝2a_ABs_AB，

对BC段有vC(2)－vB(2)＝2a_BCs_BC，s_BC＝1.6 m，由以上各式解得s_AB＝6.4 m.

12．答案：(1)6.25 m/s²　2.5 m/s²　(2)87.5 m

解析：(1)先研究货车，设货车的运动时间为t，则有

x₁＝v₁t₀＋2(v1(t－t0))

代入数据可得t＝4.5 s

货车减速运动的加速度大小为

a₁＝t－0.5 s(v1)＝2.5 m/s²

小轿车减速运动的加速度大小为

a₂＝t－0.5 s(v2)＝6.25 m/s²

(2)由题意可得小轿车的位移大小

x₂＝v₂t₀＋2(v2(t－t0))＝62.5 m

刚发现对方时两车间的距离为x＝x₁＋x₂＝87.5 m

13．答案：(1)0　55 m　(2)见解析　(3)55 m

解析：(1)由题图1可知，甲车在0～3 s内做匀减速直线运动

初速度v₀＝108 km/h＝30 m/s

则3 s末，甲车的速度为v＝v₀－at＝30 m/s－10×3 m/s＝0

甲车的位移为x₁＝0()＝－20(0－900) m＝45 m

由题图2可知，0～3 s内，乙车做匀速直线运动，乙车的位移为x₂＝v₀t＝30×3 m＝90 m

则t＝3 s时，两车相距的距离为Δx＝x₁＋x₀－x₂＝55 m

(2)t＝3 s后，甲车做初速度为零的匀速直线运动，乙车做初速度为30 m/s的匀减速直线运动，且两车在t＝3 s时相距55 m

当两车的速度相等时有a_甲t′＝v₀＋a_乙t′

其中a_甲＝5 m/s²，a_乙＝－5 m/s²

解得t′＝3 s

此过程甲的位移为x_甲＝2(1)a_甲t′²＝2(1)×5×9 m＝22.5 m

乙的位移为x_乙＝v₀t′＋2(1)a_乙t′²＝30×3 m－2(1)×5×9 m＝67.5 m

因为x_乙－x_甲＝45 m<55 m，故两车不会相撞

(3)根据题图2,9 s末，v_乙 ＝v₀＋a_乙t″

可以得到乙车在9 s末的速度为零，则3～9 s内

乙车的位移x′₁＝0()＝－2×5(0－900) m＝90 m

甲车的位移x′₂＝2(1)a_甲t″²＝2(1)×5×36 m＝90 m

则两车在9 s时的间距Δx＝x₂′＋55 m－x′₁＝55 m