3.1.1两角和与差的余弦公式

一、知识归纳：

1、两角和与差的余弦公式：

二、例题选讲：

例1、计算①；               ②；      

例2、①已知求的值；

②已知，求的值。

例3、求值：

（1）；

（2）。

3.1.2两角和与差的正弦、正切公式

一、知识归纳：

1、两角和与差的正弦公式：

2、两角和与差的正切公式：

二、例题选讲：

例1、利用和（差）角公式计算下列各式的值

（1）         （2）

例3、求下列各式的值：

（1）tan17°+tan28°+tan17°tan28°

（2）已知，求的值。

两角和与差的正弦、余弦和正切公式

一、知识归纳：

1、辅助角公式:

  (，)

2、已知三角函数值求角

二、例题精讲：

例1、化简下列各式

（1）=                    （2）=

（3）=

例2、（1）已知cos（α-）+sinα=

A.-　　　　B.          C.-           D.  

（2）_________

例3、已知三角函数值求角   

1)已知锐角、满足，，求+

2)若则=           

3)若，且、为锐角，求

3.1.3  二倍角的正弦、余弦、正切公式（1）

一、 知识归纳：

二倍角公式：

二、 例题精解：

例1、已知，求的值。

例2、已知, （1）求的值。 （2）求的值。

例3、若

例4、已知

3.1.3 二倍角的正弦、余弦、正切公式（2）

一、知识归纳：

1、二倍角公式：

2、升降幂公式：

二、例题精解：

例1、求值

例2、化简（1）

（2）

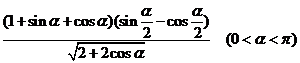
例3、化成y＝Asin(ωx＋)+k形式

（1）   （2）    

（3）     （5）

例4、求值

三角函数图像性质

1.．

（Ⅰ）求的****值，并求出此时x的值；

（Ⅱ）写出的单调递增区间,对称轴，对称中心．

2.已知＝（1＋，1），＝（1，）（，∈R），且·.

（Ⅰ）求函数的最小正周期及对称轴；

（Ⅱ）若的****值是4，求的值，并说明此时的图象可由的图象经过怎样的变换而得到.

3.已知函数的最小正周期为，且当时，函数取****值.

（1）求的解析式，并判断函数的奇偶性；

（2）试列表描点作出在[0，]范围内的图象.

4.已知函数f(x)＝为偶函数，且函数y＝f(x)图象的两相邻对称轴间的距离为

（Ⅰ）求f（）的值；

（Ⅱ）将函数y＝f(x)的图象向右平移个单位后，再将得到的图象上各点的横坐标伸长到原来的4倍，纵坐标不变，得到函数y＝g(x)的图象，求g(x)的单调递减区间.