空间垂直关系学案（1）

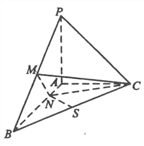
1.已知三棱锥P－ABC中，PA⊥ABC，AB⊥AC，PA=AC=½AB，N为AB上一点，AB=4AN,M,S分别为PB,BC的中点，证明：CM⊥SN；

2.如图，在三棱锥中，⊿是等边三角形，∠PAC=∠PBC=90 º，证明：AB⊥PC

3.在直四棱柱中，底面满足条件           时，有.(只需填一个条件)

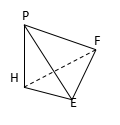
4．已知PH⊥Rt△HEF所在的平面，且HE⊥EF，连结PE、PF，

则图中直角三角形的个数是（    ）

 A  1   B 2      C  3     D 4

5．在直三棱柱中，平面侧面，求证：；

6.在直三棱柱ABC—A1B1C1中，B1C1=A1C1，A1B⊥AC1，求证：A1B⊥B1C

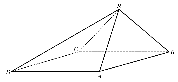7.四棱锥S－ABCD中，底面ABCD为平行四边形，侧面SBC⊥底面ABCD。已知∠ABC＝45°，AB＝2，BC=2，SA＝SB，证明：SA⊥BC；

8． 在四棱锥P—ABCD中，底面ABCD是矩形，AB=2，BC=a，又侧棱PA⊥底面ABCD

（1）当a为何值时，BD⊥平面PAC?试证明你的结论

（2）当a=4时，求证：BC边上存在一点M，使得PM⊥DM

9.已知斜三棱柱ABC—A1B1C1中，A1C1=B1C1=2，D、D1分别是AB、A1B1的中点，平面A1ABB1⊥平面A1B1C1，异面直线AB1和C1B互相垂直.

(1)求证：AB1⊥C1D1；(2)求证：AB1⊥面A1CD；

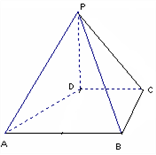10. 如图，在四棱锥P-ABCD中，PD⊥平面ABCD，PD=DC=BC=1，AB=2，AB∥DC，∠BCD=900。

(1)求证：PC⊥BC；

(2)求点A到平面PBC的距离。

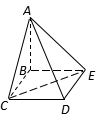11. 四棱锥中，底面为矩形，侧面底面，，，．证明：；

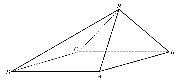12.四棱锥S－ABCD中，底面ABCD为平行四边形，侧面SBC⊥底面ABCD。已知∠ABC＝45°，AB＝2，BC=2，SA＝SB，证明：SA⊥BC；

7月10日    空间角的计算

一.  例题精讲

1.正三棱椎S—ABC的侧棱与底边相等，E、F是SC、AB中点，则异面直线EF与SA所成的角等于          

2.正方体ABCD——A1B1C1D1棱长为1，M、N分别是A1B1与BB1中点，则AM与CN所成角的余弦值是                

3. 正方形ABCD与正方形ABEF所在平面成60。二面角，则AD与BF所成角的余弦值是        

4． 如图，在四棱锥P—ABCD中，底面ABCD为矩形，侧棱PA⊥底面ABCD，AB=，BC=1，PA=2，E为PD的中点.

（Ⅰ）求直线AC与PB所成角的余弦值； 

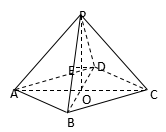5.在四棱锥P－ABCD中，底面是边长为2的菱形，∠DAB＝60，对角线AC与BD相交于点O，PO⊥平面ABCD，PB与平面ABCD所成的角为60．

（1）求四棱锥P－ABCD的体积；

（2）若E是PB的中点，求异面直线DE与PA所成角的大小

6.如图，在四棱锥P-ABCD中，底面为直角梯形,AD∥BC,∠BAD=90°,PA⊥底面ABCD，且PA＝AD=AB=2BC,M、N分别为PC、PB的中点.(Ⅰ)求证：PB⊥DM; (Ⅱ)求CD与平面ADMN所成的角。

7．正三棱椎S—ABC的侧棱与底边相等，E、F是SC、AB中点，则异面直线SF与BE所成的角等于                  

8．正方体ABCD——A1B1C1D1棱长为1，M、N分别是A1B1与BB1中点，则AM与, DN所成角的余弦值是                                  

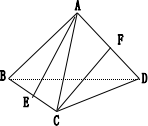9．已知正四面体ABCD中，E、F分别为BC、AD的中点，连AE、CF。

（1）求异面直线AE与CF所成角的大小；

（2）求CF与平面BCD所成角的大小。

10．已知正方体ABCD-A1B1C1D1，E、F、G分别是AB、C1D1、B1C1的中点，求：

（1）求平面AFG和平面AB1D1所成的角

（2）求二面角B1-A1C-C1

11．过正方形ABCD的顶点A作PA⊥平面ABCD，设PA＝AB＝ａ；

（1）求二面角B－PC－D的大小；（2）求平面PAB和平面PCD所成二面角的大小。

 

 

 

 

 

12．如图，已知四棱锥的底面是直角梯形，

，侧面底面． 

（1）与是否相互垂直，请证明你的结论；

（2）求二面角的大小