直线 7月11日
1.已知A(-2,a),B(1,3),C(4,-6)三点共线,则a= , 斜率= , 倾斜角=
2.求直线方程:(1)直线![]() 的倾斜角是直线
的倾斜角是直线![]() 的2倍,且它在y轴上的截距为1,求直线
的2倍,且它在y轴上的截距为1,求直线![]() 的方程。(2)求过点A(3,2),且在两坐标轴上截距相等的直线方程。
的方程。(2)求过点A(3,2),且在两坐标轴上截距相等的直线方程。
(3)过点P(2,1)作直线![]() 交x、y轴正半轴于A、B两点,
交x、y轴正半轴于A、B两点,
1) 当![]() 取到最小值时,求直线
取到最小值时,求直线![]() 的方程。
的方程。
2) 当![]() 的面积取到最小值时,求直线
的面积取到最小值时,求直线![]() 的方程。
的方程。
3.若直线![]() 过P(3,2)点,倾斜角是直线
过P(3,2)点,倾斜角是直线![]() 的倾斜角的2倍,则该直线方程是_________________________.
的倾斜角的2倍,则该直线方程是_________________________.
4.已知直线![]() 过点M(-5,3),且倾斜角α的正弦值为
过点M(-5,3),且倾斜角α的正弦值为![]() ,求直线
,求直线![]() 的方程。
的方程。
5.若一直线被两条已知直线4x+y+6=0和3x-5y-6=0截得的线段的中点恰好在坐标原点,求这条直线的方程。
6.(1)已知两直线![]() :(m+3)x+5y=5-3m,
:(m+3)x+5y=5-3m, ![]() :2x+(m+6)y=8,当m为何值时
:2x+(m+6)y=8,当m为何值时![]() 与
与![]()
1)相交; 2)平行; 3)重合; 4)垂直
(2)已知直线![]() 的方程为
的方程为![]() ,求直线
,求直线![]() 的方程:
的方程:
1)![]() 与
与![]() 平行,且过点(-1,3);
平行,且过点(-1,3);
2)![]() 与
与![]() 垂直,且
垂直,且![]() 与坐标轴围成的三角形面积为4.
与坐标轴围成的三角形面积为4.
7.等腰直角三角形![]() 的直角边
的直角边![]() 所在直线方程为
所在直线方程为![]() ,顶点
,顶点![]() ,求斜边
,求斜边![]() 及直角边
及直角边![]() 所在直线的方程.
所在直线的方程.
8. 已知点P(2,-1),求:
1)过P点与原点距离为2的直线![]() 的方程;
的方程;
2)过P点与原点距离****的直线![]() 的方程,****距离是多少?
的方程,****距离是多少?
3)是否存在过P点与原点距离为6的直线?若存在,求出方程;若不存在,请说明理由
9.求点P(3,-2)到下列直线的距离:1)y=![]() ; 2)y=6; 3)y轴
; 2)y=6; 3)y轴![]()
10..若直线![]() :
:![]() 与直线
与直线![]() :
:![]() 平行且不重合,则
平行且不重合,则![]() 的值是 .
的值是 .
11.过点![]() 且垂直于直线
且垂直于直线![]() 的直线方程为
的直线方程为
12.已知直线l经过点P(1,2),且被两平行直线l1:4x+3y+1=0和l2:4x+3y+6=0截得的线段之长为![]() ,求直线l的方程.
,求直线l的方程.
线性规划
1.(1)画出不等式组表示的平面区域: 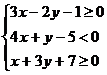
(2)在坐标平面上,不等式组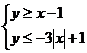 所表示的平面区域的面积为
所表示的平面区域的面积为
2.(1))设![]() 满足约束条件
满足约束条件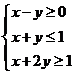 ,则
,则![]() 的****值为
的****值为
(2)已知点![]() 在不等式组
在不等式组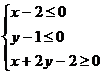 表示的平面区域内,则
表示的平面区域内,则![]() 的取值范围是
的取值范围是
(3)已知实数![]() 满足
满足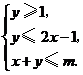 如果目标函数
如果目标函数![]() 的最小值为
的最小值为![]() ,则实数
,则实数![]() 等于
等于
(4)已知平面区域D由以![]() 为顶点的三角形内部&边界组成。若在区域D上有无穷多个点
为顶点的三角形内部&边界组成。若在区域D上有无穷多个点![]() 可使目标函数
可使目标函数![]() 取得最小值,则
取得最小值,则![]()
(5)设![]() 满足条件
满足条件 ,则
,则![]() 的****值是
的****值是
3.原点和点![]() 在直线
在直线![]() 的两侧,则
的两侧,则![]() 的取值范围是 .
的取值范围是 .
4.若实数![]() 满足
满足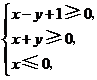 则
则![]() 的最小值是
的最小值是
5. 实数x,y满足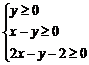 ,则t=
,则t=![]() 的取值范围是
的取值范围是
6.已知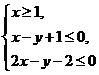 则
则![]() 的最小值是
的最小值是
等差数列 7月12日
1.在等差数列![]() 中,
中,![]() ,则
,则![]() .
.
2.等差数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() 则
则![]()
3.设等差数列![]() 的前
的前![]() 项和为
项和为![]() ,若
,若![]() 则
则![]() .
.
4.已知![]() 是等差数列,
是等差数列,![]() ,
,![]() ,则该数列前10项和
,则该数列前10项和![]() 等于( )
等于( )
A.64 B.100 C.110 D.120
5.已知两个等差数列![]() 和
和![]() 的前
的前![]() 项和分别为A
项和分别为A![]() 和
和![]() ,且
,且![]() ,则使得
,则使得![]() 为整数的正整数
为整数的正整数![]() 的个数是( )
的个数是( )
A.2 B.3 C.4 D.5
6.已知等差数列共有10项,其中奇数项之和15,偶数项之和为30,则其公差是( )
A.5 B.4 C. 3 D.2
7.若![]() 是等差数列,首项
是等差数列,首项![]() ,则
,则
使前n项和![]() 成立的****自然数n是( )
成立的****自然数n是( )
A.4005 B.4006 C.4007 D.4008
8.设![]() 是公差不为零的等差数列,
是公差不为零的等差数列,![]() 为其前
为其前![]() 项和,满足
项和,满足![]() 。
。
(1)求数列![]() 的通项公式及前
的通项公式及前![]() 项和
项和![]() ;
; ![]()
9.在数列![]() 中,
中,![]() ,
,![]() .
.
(Ⅰ)设![]() .证明:数列
.证明:数列![]() 是等差数列;
是等差数列;
10.已知{an}是一个公差大于0的等差数列,且满足a3a6=55, a2+a7=16.
(Ⅰ)求数列{an}的通项公式:
11.设Sn是等差数列{an}的前n项和,若=3,则=( )
(A)10 (B)3 (C)8 (D)9
12.已知数列![]() 、
、![]() 都是公差为1的等差数列,其首项分别为
都是公差为1的等差数列,其首项分别为![]() 、
、![]() ,且
,且![]() ,
,![]() .设
.设![]() (
(![]() ),则数列
),则数列![]() 的前10项和等于( )
的前10项和等于( )
A.55 B.70 C.85 D.100
13.已知等差数列{![]() }中,
}中,![]()
![]() 求{
求{![]() }前n项和
}前n项和![]() .
.