7月12日  §3.2.1古典概型

一、知识归纳

1.基本事件：

2. 基本事件的特点

3.古典概型：

4.古典概型的概率公式

二、基本例题

例1、从字母中任意取出两个不同字母的实验中，有哪些基本事件？

例2、单选题是标准化考试中常用的题型，一般是从四个选项中选择一个正确答案。如果考生掌握了考察的内容，他可以选择****正确的答案。假设考生不会做，他随机的选择一个答案，问他答对的概率是多少？

例3、同时掷两个骰子，计算：

（1） 一共有多少种不同的结果？

（2） 其中向上的点数之和是5的结果有多少种？

（3） 其中向上的点数之和是5的概率是多少？

例4、假设储蓄卡的密码由4个数字组成，每个数字可以是0，1，2，……,9十个数字中的任意一个。假设一个人****忘记了自己的储蓄卡密码，问他到自动取款机上随机试一次密码就能取到钱的概率是多少？

例5、某种饮料每箱装6听，如果其中有2听不合格，问质检人员从中随机抽出2听，检测出不合格产品的概率有多大？

针对训练

三、1、做透支二颗子的试验：用表示结果，其中表示第1颗骰子出现的点数，表示第2颗骰子出现的点数，写出

（1）试验的基本事件       （2）“出现点数之和大于8”的事件

（3）“出现点数相等”的事件              （4）“出现点数之和大于10”的事件

3、任意投掷两枚骰子，计算

（1）出现点数相同的概率

（2）出现点数之和为奇数的概率

（3）出现点数之和为偶数的概率

           §3.2.2（整数值）随机数的产生

一、基本例题

例1、天气预报说，在今后的三天中，每一天下雨的概率均为40%，这三天中恰有两天下雨的概率大概是多少？

例2、盒中有大小形状相同的5只白球，2只黑球，用随机模拟法，设计一个随机模拟试验，估计下列事件的概率

（1） 任取一球，得到白球

（2） 任取三球，恰有2只白球

（3） 任取三球（分三次每次放回再取）恰有3只白球

例3、某人有5把钥匙，其中2把能打开门，现随机地取1把钥匙试着开门，不能打开门就扔掉，问第三次才打开门的概率是多大？如果试过的钥匙不扔掉，这个概率又是多少？设计一个随机模拟试验，估计上述事件发生的概率

§3.3.1几何概型

一、知识归纳

  1几何概型

  2几何概型的计算公式

二、例题精讲

例1 判断下列实验是否为几何概型，并说明理由

（1） 明天某个地方降水的概率。

（2） 设A为圆周上一定点，在圆周上等可能任取一点与A连接，求弦长超过半径的概率。

例2 在长为12的线段AB上任取一点M，并以线段AM为边作正方形，求正方形的面积介于36与48之间的概率。

例3 在正方体内任取一点，求该点在正方体的内切球内的概率。

三、针对训练

1、在[0，3]上任取一个数，求这个数大于0.5而小于1.5的概率。

2、将一长为18的线段随机分为三段，则这三段线段能组成一个三角形的概率是多少。

3、一个球形容器半径为3cm，里面装满纯净水，不小心混入一个病毒，从中任取1ml水，则病毒留在容器中的概率是多少。

4、取一根长度为3m的绳子，拉直后在任意位置剪断，，那么剪的两段的长度都不小于1m的概率是（    ）

A 、2/3        B 、1/3        C 、1/4        D、不能确定

5、在线段[0，3］上任取一点，则此点坐标大于1的概率是（    ）

A 、1/3   B 、2/3    C、1/2     D、1/3

6、某人睡午觉醒来，发觉表停了，他打开收音机想听电台整点报时，假定电台每小时报时一次，则他等待的时间不长于10min的概率是           。  

7、在一万平方千米的海域中有40平方千米的大陆架储藏着石油，假如在海域中任意一点钻探，那么钻到石油层的概率是                      。

8、在1000mL的水中有一条蚊子幼虫，现从中随意取出10mL水样放到显微镜下观察，则发现蚊子幼虫的概率是               。

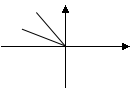
9、如图所示，在直角坐标系xOy内，射线OT落在120°的终边上，任作一条射线OA，则射线OA落在∠xOT内的概率为                  。

10、，在一个边长为5cm的正方形内部画一个边长为3cm的小正方形，向大正方形内随机投点，则所投的点落入小正方形内的概率为                。

11、向面积为9的ABC内任投一点P,那么PBC的面积小于3的概率是        。

12、已知地铁列车每10分钟一班，在车站停1分钟，则乘客到达站台立即乘上车的概率是                    。

13、在等腰RtABC中，在线段斜边AB上任取一点M，则AM的长小于AC的长的概率是                   。

7月13日1．1．2 (1)程序框图

知识归纳

一.（1）起止框图：      （2）输入、输出框：     

（3）处理框：      （4）判断框：             （5）流程线：    （6）连接点 

二.（1）顺序结构（2）判断结构  

例题精讲

例1：已知x=4,y=2,画出计算w=3x+4y的值的程序框图。

例2：已知一个三角形的三边分别为2、3、4，利用海伦公式设计一个算法，求出它的面积，并画出算法的程序框图。

例3.任意给定3个正实数，设计一个算法，判断以这3个正实数为三条边边长的三角形

是否存在，并画出这个算法的程序框图．

例4 设计一个求解一元二次方程的算法，并画出程序框图表示

针对训练

1.利用梯形的面积公式计算上底为，下底为，高为的梯形的面积．设计出该问题

的算法及程序框图．

2．已知函数编写一程序求函数值．

3．某电信部门规定：拨打市内电话时，如果通话时间不超过3分钟，则收取通话费0.2元，如果通话时间超过3分钟，则超过部分以每分钟0.1元收取通话费（通话不足1分钟按1分钟计），试设计一个计算通话费用的算法．（要求写出算法，画出程序框图，编写程序）

4.一个三位数,如果每一位数字的立方和等于它本身,则称之为“水仙花数”．设计一个算法，