第二章　章末检测

(时间：120分钟　满分：150分)

一、选择题(本大题共12小题，每小题5分，共60分)

1．(2010·宁德四县市一中联考)已知集合A＝{x|y＝lg(2x－x²)}，B＝{y|y＝2^x，x>0}，R是实数集，则(∁_RB)∩A等于                                                  (　　)

A．[0,1]                                                  B．(0,1]

C．(－∞，0]                                           D．以上都不对

2．下列四个函数中，与y＝x表示同一函数的是                              (　　)

A．y＝()²                                             B．y＝

C．y＝                                               D．y＝

3．设a＝log₃π，b＝log₂，c＝log₃，则                                   (　　)

A．a>b>c                                                B．a>c>b

C．b>a>c                                                D．b>c>a

4．(2010·吉安高三联考)由方程x|x|＋y|y|＝1确定的函数y＝f(x)在(－∞，＋∞)上是 (　　)

A．增函数                                               B．减函数

C．先增后减                                           D．先减后增

5．函数f(x)＝|x|－k有两个零点，则                                        (　　)

A．k＝0                                                  B．k>0

C．0≤k<1                                               D．k<0

6．若0<x<y<1，则                                                       (　　)

A．3^y<3^x                                                  B．log_x3<log_y3

C．log₄x<log₄y                                         D．()^x<()^y

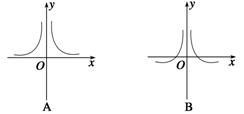
7．(2011·新乡月考)函数y＝的图象大致是                               (　　)

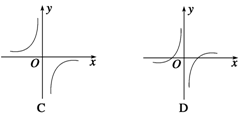
8．(2010·天津)若函数f(x)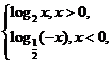＝若f(a)>f(－a)，则实数a的取值范围(　　)

A．(－1,0)∪(0,1)                                    B．(－∞，－1)∪(1，＋∞)

C．(－1,0)∪(1，＋∞)                             D．(－∞，－1)∪(0,1)

9．(2011·张家口模拟)已知幂函数f(x)的图象经过点(，)，P(x₁，y₁)，Q(x₂，y₂)(x₁<x₂)是函数图象上的任意不同两点，给出以下结论：

①x₁f(x₁)>x₂f(x₂)；

②x₁f(x₁)<x₂f(x₂)；

③>；

④<.

其中正确结论的序号是                                                 (　　)

A．①②                                                  B．①③

C．②④                              &nb, sp;                   D．②③

10．(2010·山西阳泉、大同、晋中5月联考)已知函数f(x)＝的值域为[0，＋∞)，则它的定义域可以是                                             (　　)

A．(0,1]                                                  B．(0,1)

C．(－∞，1]                                           D．(－∞，0]

11．已知定义在R上的奇函数f(x)，满足f(x－4)＝－f(x)，且在区间[0,2]上是增函数，(　　)

A．f(－25)<f(11)<f(80)                             B．f(80)<f(11)<f(－25)

C．f(11)<f(80)<f(－25)                             D．f(－25)<f(80)<f(11)

12．已知a>0且a≠1，f(x)＝x²－a^x，当x∈(－1,1)时，均有f(x)<，则实数a的取值范围是                                                                     (　　)

A．(0，]∪[2，＋∞)                             B．[，1)∪(1,4]

C．[，1)∪(1,2]                                     D．(0，]∪[4，＋∞)

二、填空题(本大题共4小题，每小题5分，共20分)

13．已知对不同的a值，函数f(x)＝2＋a^x－1(a>0，且a≠1)的图象恒过定点P，则P点的坐标是________．

14．(2011·南京模拟)定义在R上的函数f(x)满足f(x)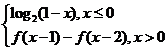＝，则

f(2 011)的值为__________．

15．定义：区间[x₁，x₂](x₁<x₂)的长度为x₂－x₁.已知函数y＝|log_0.5x|的定义域为[a，b]，值域为[0,2]，则区间[a，b]的长度的****值为________．

16．(2011·潍坊模拟)设函数f(x)是定义在R上的偶函数，且对任意的x∈R恒有f(x＋1)＝f(x－1)，已知当x∈[0,1]时f(x)＝()^1－x，则

①2是函数f(x)的周期；

②函数f(x)在(1,2)上是减函数，在(2,3)上是增函数；

③函数f(x)的****值是1，最小值是0；

④当x∈(3,4)时，f(x)＝()^x－3.

其中所有正确命题的序号是________．

三、解答题(本大题共6小题，共70分)

17．(10分)(2011·合肥模拟)对定义在实数集上的函数f(x)，若存在实数x₀，使得f(x₀)＝x₀，那么称x₀为函数f(x)的一个不动点．

(1)已知函数f(x)＝ax²＋bx－b(a≠0)有不动点(1,1)、(－3，－3)，求a、b；

(2)若对于任意实数b，函数f(x)＝ax²＋bx－b (a≠0)总有两个相异的不动点，求实数a的取值范围．

18．(12分)已知f(x)为定义在[－1,1]上的奇函数，当x∈[－1,0]时，函数解析式f(x)＝－(a∈R)．

(1)写出f(x)在[0,1]上的解析式；

(2)求f(x)在[0,1]上的****值．

19．(12分)已知函数f(x)＝2^x－.

(1)若f(x)＝2，求x的值；

(2)若2^tf(2t)＋mf(t)≥0对于t∈[1,2]恒成立，求实数m的取值范围．

20．(12分)(2011·银川模拟)已知函数f(x)的图象与函数h(x)＝x＋＋2的图象关于点A(0,1)对称．

(1)求函数f(x)的解析式；

(2)若g(x)＝f(x)＋，g(x)在区间(0,2]上的值不小于6，求实数a的取值范围．

21．(12分)经市场调查，某城市的一种小商品在过去的近20天内的销售量(件)与价格(元)均为时间t(天)的函数，且销售量近似满足g(t)＝80－2t(件)，价格近似满足f(t)＝20－|t－10|(元)．

(1)试写出该种商品的日销售额y与时间t(0≤t≤20)的函数表达式；

(2)求该种商品的日销售额y的****值与最小值．

22．(12分)(2011·合肥模拟)对于定义域为[0,1]的函数f(x)，如果同时满足以下三条：①对任意的x∈[0,1]，总有f(x)≥0；②f(1)＝1；③若x₁≥0，x₂≥0，x₁＋x₂≤1，都有f(x₁＋x₂)≥f(x₁)＋f(x₂)成立，则称函数f(x)为理想函数．

(1)若函数f(x)为理想函数，求f(0)的值；

(2)判断函数f(x)＝2^x－1 (x∈[0,1])是否为理想函数，并予以证明；

(3)若函数f(x)为理想函数，假定存在x₀∈[0,1]，使得f(x₀)∈[0,1]，且f[f(x₀)]＝x₀，求证：f(x₀)＝x₀.

答案  1．B　[由2x－x²>0，

得x(x－2)<0⇒0<x<2，

故A＝{x|0<x<2}，由x>0，得2^x>1，

故B＝{y|y>1}，∁_RB＝{y|y≤1}，

则(∁_RB)∩A＝{x|0<x≤1}．]

2．B

3．A　[∵log₃<log₂<log₂，∴b>c.

又∵log₂<log₂2＝log₃3<log₃π，

∴a>b，∴a>b>c.]

4．B　[

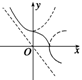
①当x≥0且y≥0时，

x²＋y²＝1，

②当x>0且y<0时，x²－y²＝1，

③当x<0且y>0时，y²－x²＝1，

④当x<0且y<0时，无意义．

由以上讨论作图如右，易知是减函数．]

5．B　[令y＝|x|，y＝k，由题意即要求两函数图象有两交点，利用数形结合思想，作出两函数图象，得k>0.]

6．C　[∵0<x<y<1，∴由函数的单调性得3^x<3^y，log_x3>log_y3，()^x>()^y，即选项A、B、D错，故选C.]

7．D

8．C　[由分段函数的表达式知，需要对a的正负进行分类讨论．

f(a)>f(－a)⇒或

⇒或

⇒a>1或－1<a<0.]

9．D　[依题意，设f(x)＝x^α，则有()^α＝，即()^α＝()，所以α＝，于是f(x)＝x.

由于函数f(x)＝x在定义域[0，＋∞)内单调递增，所以当x₁<x₂时，必有f(x₁)<f(x₂)，从而有x₁f(x₁)<x₂f(x₂)，故②正确；又因为，分别表示直线OP、OQ的斜率，结合函数图象，容易得出直线OP的斜率大于直线OQ的斜率，故>，所以③正确．]

10．A　[∵f(x)的值域为[0，＋∞)，

令t＝4^x－2^x＋1＋1，

∴t∈(0,1]恰成立，即0<(2^x)²－2·2^x＋1≤1恰成立，0<(2^x－1)²成立，则x≠0，(2^x)²－2·2^x＋1≤1可化为2^x(2^x－2)≤0，

∴0≤2^x≤2，即0≤x≤1，

综上可知0<x≤1.]

11．D　[因为f(x)满足f(x－4)＝－f(x)，所以f(x－8)＝f(x)，所以函数是以8为周期的周期函数，则f(－25)＝f(－1)，f(80)＝f(0)，f(11)＝f(3)，又因为f(x)在R上是奇函数，f(0)＝0得f(80)＝f(0)＝0，f(－25)＝f(－1)＝－f(1)，而由f(x－4)＝－f(x)得f(11)＝f(3)＝－f(－3)＝－f(1－4)＝f(1)，又因为f(x)在区间[0,2]上是增函数，所以f(1)>f(0)＝0，－f(1)<0，即f(－25)<f(80)<f(11)．]

12．C　[将f(x)<化为x²－<a^x，利用数形结合，分a>1和0<a<1两种情况求解．

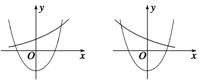
结合图象得或，

解得1<a≤2或≤a<1.]

13．(1,3)

14．－1

解析　由已知得f(－1)＝log₂2＝1，

f(0)＝0，f(1)＝f(0)－f(－1)＝－1，

f(2)＝f(1)－f(0)＝－1，

f(3)＝f(2)－f(1)＝－1－(－1)＝0，

f(4)＝f(3)－f(2)＝0－(－1)＝1，

f(5)＝f(4)－f(3)＝1，f(6)＝f(5)－f(4)＝0，

所以函数f(x)的值以6为周期重复性出现，

所以f(2 011)＝f(1)＝－1.

15.

解析　由0≤|log_0.5x|≤2解得≤x≤4，

∴[a，b]长度的****值为4－＝.

16．①②④

解析　由f(x＋1)＝f(x－1)可得f(x＋2)＝f[(x＋1)＋1]＝f(x＋1－1)＝f(x)，

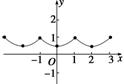
∴2是函数f(x)的一个周期．

又函数f(x)是定义在R上的偶函数，

且x∈[0,1]时，

f(x)＝()^1－x，

∴函数f(x)的简图如右图，由简图可知②④也正确．

17．解　(1)∵f(x)的不动点为(1,1)、(－3，－3)，

∴有∴a＝1，b＝3.………………………………………………(4分)

(2)∵函数总有两个相异的不动点，

∴ax²＋(b－1)x－b＝0，Δ>0，

即(b－1)²＋4ab>0对b∈R恒成立，……………………………………………………(7分)

Δ₁<0，即(4a－2)²－4<0，………………………………………………………………(9分)

∴0<a<1.…………………………………………………………… …………………(10分)

18．解　(1)∵f(x)为定义在[－1,1]上的奇函数，且f(x)在x＝0处有意义，

∴f(0)＝0，即f(0)＝－＝1－a＝0.

∴a＝1.……………………………………………………………………………………(3分)

设x∈[0,1]，则－x∈[－1,0]．

∴f(－x)＝－＝4^x－2^x.

又∵f(－x)＝－f(x)

∴－f(x)＝4^x－2^x.

∴f(x)＝2^x－4^x.……………………………………………………………………………(8分)

(2)当x∈[0,1]，f(x)＝2^x－4^x＝2^x－(2^x)²，

∴设t＝2^x(t>0)，则f(t)＝t－t².

∵x∈[0,1]，∴t∈[1,2]．

当t＝1时，取****值，****值为1－1＝0.……………………………………………(12分)

19．解　(1)当x<0时，f(x)＝0；

当x≥0时，f(x)＝2^x－.…………………………………………………………………(3分)

由条件可知2^x－＝2，即2^2x－2·2^x－1＝0，

解得2^x＝1±.

∵2^x>0，∴x＝log₂(1＋)．……………………………………………………………(6分)

(2)当t∈[1,2]时，2^t＋m≥0，

即m(2^2t－1)≥－(2^4t－1)．

∵2^2t－1>0，∴m≥－(2^2t＋1)．…………………………………………………………(9分)

∵t∈[1,2]，∴－(1＋2^2t)∈[－17，－5]，

故m的取值范围是[－5，＋∞)．……………………………………………………(12分)

20．解　(1)设f(x)图象上任一点坐标为(x，y)，点(x，y)关于点A(0,1)的对称点(－x,2－y)在h(x)的图象上，……………………………………………………………………………(2分)

∴2－y＝－x＋＋2，∴y＝x＋，

即f(x)＝x＋.……………………………………………………………………………(6分)

(2)由题意g(x)＝x＋，

且g(x)＝x＋≥6，x∈(0,2]．

∵x∈(0,2]，∴a＋1≥x(6－x)，…………………………………………………………(8分)

即a≥－x²＋6x－1.

令q(x)＝－x²＋6x－1，x∈(0,2]，

q(x)＝－x²＋6x－1＝－(x－3)²＋8，

∴x∈(0,2]时，q(x)_max＝q(2)＝7，∴a≥7.……………………………………………(12分)

21．解　(1)y＝g(t)·f(t)＝(80－2t)·(20－|t－10|)＝(40－t)(40－|t－10|)

＝……………………………………………………(4分)

(2)当0≤t<10时，y的取值范围是[1 200,1 225]，

在t＝5时，y取得****值为1 225；……………………………………………………(8分)

当10≤t≤20时，y的取值范围是[600,1 200]，

在t＝20时，y取得最小值为600.

所以第5天，日销售额y取得****值为1 225元；

第20天，日销售额y取得最小值为600元．………………………………………(12分)

22．(1)解　取x₁＝x₂＝0，

可得f(0)≥f(0)＋f(0)⇒f(0)≤0.

又由条件①得f(0)≥0，故f(0)＝0.………………………………………………………(4分)

(2)解　显然f(x)＝2^x－1在[0,1]满足条件①f(x)≥0；

也满足条件②f(1)＝1.

若x₁≥0，x₂≥0，x₁＋x₂≤1，

则f(x₁＋x₂)－[f(x₁)＋f(x₂)]＝2x₁＋x₂－1－[(2x₁－1)＋(2x₂－1)]＝2x₁＋x₂－2x₁－2x₂＋1＝(2x₂－1)(2x₁－1)≥0，即满足条件③，故f(x)是理想函数．………………………………(8分)

(3)证明　由条件③知，任给m、n∈[0,1]，

当m<n时，n－m∈[0,1]，

∴f(n)＝f(n－m＋m)≥f(n－m)＋f(m)≥f(m)．

若x₀<f(x₀)，则f(x₀)≤f[f(x₀)]＝x₀，前后矛盾．

若x₀>f(x₀)，则f(x₀)≥f[f(x₀)]＝x₀，前后矛盾．

故f(x₀)＝x₀.……………………………………………………………………………(12分)