第4课 函数的概念及其表示法

(本课对应学生用书第8-10页)

自主学习　回归教材

1. 函数的概念

设A,B是两个非空的数集,如果按某个确定的对应关系f,使对于集合A中的每一个元素x,在集合B中都有****的元素y和它对应,那么称f:A→B为从集合A到集合B的一个函数,记作:y=f(x),x∈A.其中所有的输入值x组成的集合A叫作函数y=f(x)的定义域;所有输出值y组成的集合叫作函数的值域.

2. 函数的相等

函数的定义含有三个要素,即定义域、值域和对应法则.

当函数的定义域及对应法则确定之后,函数的值域也就随之确定.当且仅当两个函数的定义域和对应法则都分别相同时,这两个函数才是同一个函数.

3. 函数的表示法:解析法、列表法和图象法.

1. (必修1P26练习5改编)若函数f(x)=x-x²,则f(x+1)-f(x)=　　　　.

[答案]-2x

2. (必修1P35习题7改编)已知函数y=那么使函数值为5的x的值是　　　.

[答案]-2

[解析]当x>0时,y<0,y≠5;当x≤0时,由x²+1=5,得x=-2.

3. (必修1P26习题4改编)设集合A={x|1≤x≤2},B={x|1≤x≤4},有以下4个对应法则:

①f:x→y=x²;

②f:x→y=3x-2;

③f:x→y=-x+4;

④f:x→y=4-x².

其中不能构成从A到B的函数的是　　　　.(填序号)

[答案]④

[解析]容易作出题中给出的四个函数的图象,对于函数y=4-x²,集合A中的2对应的数为0,不在集合B中.

4. (必修1P32习题7改编)已知一个函数的解析式为y=x²,它的值域为{1,4},这样的函数有　　　　个.

[答案]9

[解析]列举法:定义域可能是{1,2},{-1,2},{1,-2},{-1,-2},{1,-2,2},{-1,-2,2},{-1,1,2},{-1,1,-2},{-1,1,-2,2}.

5. (必修1P36习题9改编)小明骑车上学,开始时匀速行驶,途中因交通堵塞停留了一段时间,后为了赶时间加快速度行驶.与以上事件吻合****的图象是　　　.(填序号)

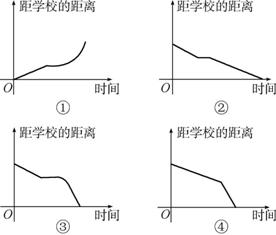
(第5题)

[答案]③