1.下列图形中不能作为函数图象的是( D )

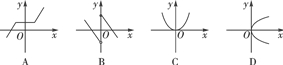
解析：根据函数定义，定义域内任何一个x取值，都有且只有****的y＝f(x)与之对应，故选D.

　2.若函数y＝f(x)的定义域是[－1,1]，则函数y＝f(log2x)的定义域是( B )

A．[－1,1]  B．[2(1)， 2]

C．[，4]  D．[1,4]

解析：由－1≤log2x≤1，得log22(1)≤log2x≤log22，由y＝log2x在(0，＋∞)上递增，得2(1)≤x≤2，故选B.

　3.若f(x)＝2x＋3，g(x＋2)＝f(x)，则g (x)的表达式为( B )

A．g(x)＝2x＋1  B．g(x)＝2x－1

C．g(x)＝2x－3  D．g(x)＝2x＋7

解析：由g(x＋2)＝f(x)，得g(x)＝f(x－2)＝2(x－2)＋3＝2x－1.

　4.(2012·广东中山市四校联考)函数y＝＋lg(3－x)(1)的定义域是　[1,2)∪(2,3)　.

解析：由lg(3－x)≠0(3－x>0)，

得1≤x<2或2<x<3.

　5.若函数f(2x＋1)＝x2－2x，则f(3)＝　－1　.

解析：(方法一)令x＝1，即得f(3)＝－1.

(方法二)先求f(x)的解析式，再求f(3)．

　6.已知f(sin α)＝cos 2α，则f(x)＝　1－2x2(|x|≤1)　.

解析：因为f(sin α)＝cos 2α＝1－2sin2α，且|sin α|≤1，

所以f(x)＝1－2x2(|x|≤1)．

　7.已知f(x)＝f(x－2)＋3 (x>1)(cos πx 　 　　(x≤1))，则f(3(7))的值为　2(7)　.

解析：f(3(7))＝f(3(7)－2)＋3＝f(3(1))＋3＝cos3(π)＋3＝2(7).

　8.已知函数φ(x)＝f(x)＋g(x)，其中f(x)是x的正比例函数，g(x)是x的反比例函数，且φ(3(1))＝16，φ(1)＝8.

(1)求φ(x)的解析式，并指出定义域；

(2)求φ(x)的值域．

解析：(1)设f(x)＝ax，g(x)＝x(b)，a、b为比例常数，

则φ(x)＝f(x)＋g (x)＝ax＋x(b)，

由φ(1)＝8()＝16)，得a＋b＝8(a＋3b＝16)，解得b＝5(a＝3).

所以φ(x)＝3x＋x(5)，其定义域为(－∞，0)∪ (0，＋∞)．

(2)由|φ(x)|＝|3x＋x(5)|＝|3x|＋|x(5)|

≥2|(5)＝2，

得φ (x)≥2或φ(x)≤－2.

所以φ(x)的值域为(－∞，－2]∪[2，＋∞)．

　9.设f(x)＝ax＋b(x)(a，b为常数，且a≠0)满足f(2)＝1，f(x)＝x有****解．

(1)求函数y＝f(x)的解析式；

(2)f[f(－3)]的值．

解析：(1)因为f(2)＝1，所以2a＋b(2)＝1，

即2a＋b＝2.①

又因为f(x)＝x有****解，即ax＋b(x)＝x有****解，

所以x·ax＋b(ax＋b－1)＝0有****解，

而x1＝0，x2＝a(1－b)，所以a(1－b)＝0，②

由①②知a＝2(1)，b＝1，

所以f(x)＝x＋1(1)＝x＋2(2x).

(2)f[f(－3)]＝f[－3＋2(2×(－3))]＝f(6)＝6＋2(2×6)＝2(3).