1.(5分)(2014秋•湛江校级期中)![]() = .
= .
2.(5分)![]() (a>0)用分数指数幂表示为 .
(a>0)用分数指数幂表示为 .
3.(5分)(2012秋•浦口区校级期末)设指数函数f(x)=(a﹣1)x是R上的减函数,则a的取值范围是 .
4.(5分)(2010•项城市校级模拟)已知幂函数y=f(x)的图象过点![]() ,则这个函数解析式为 .
,则这个函数解析式为 .
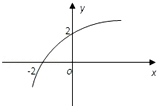
5.(5分)(2010•宿迁模拟)函数y=loga(x+b)的图象如图所示,则a+b的值为 .
1.(5分)(2014秋•湛江校级期中)![]() = π﹣3 .
= π﹣3 .
|
考点: |
方根与根式及根式的化简运算.菁优网版权所有 |
|
专题: |
计算题. |
|
分析: |
由 |
|
解答: |
解: =|3﹣π| =π﹣3 故答案为:π﹣3 |
|
点评: |
本题考查的知识点是根式的化简运算,其中掌握根式的性质 |
2.(5分)![]() (a>0)用分数指数幂表示为
(a>0)用分数指数幂表示为 ![]() .
.
|
考点: |
根式与分数指数幂的互化及其化简运算.菁优网版权所有 |
|
专题: |
计算题. |
|
分析: |
由根式和分数指数幂的互化求解即可. |
|
解答: |
解: 故答案为: |
|
点评: |
本题考查根式和分数指数幂的互化、指数的运算法则,属基本运算的考查. |
3.(5分)(2012秋•浦口区校级期末)设指数函数f(x)=(a﹣1)x是R上的减函数,则a的取值范围是 1<a<2 .
|
考点: |
指数函数的单调性与特殊点.菁优网版权所有 |
|
专题: |
计算题. |
|
分析: |
欲使得指数函数f(x)=(a﹣1)x是R上的减函数,只须其底数小于1即可,从而求得a的取值范围. |
|
解答: |
解:根据指数函数的性质得: 0<a﹣1<1, ∴1<a<2. 故答案为1<a<2. |
|
点评: |
本题主要考查了指数函数的单调性,属容易题. |
4.(5分)(2010•项城市校级模拟)已知幂函数y=f(x)的图象过点![]() ,则这个函数解析式为
,则这个函数解析式为 ![]() .
.
|
考点: |
幂函数的概念、解析式、定义域、值域.菁优网版权所有 |
|
专题: |
计算题. |
|
分析: |
根据幂函数的概念设f(x)=xα,将点的坐标代入即可求得α值,从而求得函数解析式. |
|
解答: |
解:设f(x)=xα, ∵幂函数y=f(x)的图象过点 ∴ ∴α= 这个函数解析式为 故答案为: |
|
点评: |
本题主要考查了待定系数法求幂函数解析式、指数方程的解法等知识,属于基础题. |
5.(5分)(2010•宿迁模拟)函数y=loga(x+b)的图象如图所示,则a+b的值为 ![]() .
.

|
考点: |
对数函数的图像与性质.菁优网版权所有 |
|
专题: |
数形结合. |
|
分析: |
根据图象上的特殊点的坐标值,代入函数表达式得到关于参数a,b的方程组,最后解这个方程即得a,b的值,从而求出a+b的值. |
|
解答: |
解:由图象得:
解得:
∴a+b的值为 故答案为: |
|
点评: |
本小题主要考查对数函数的图象、对数函数的图象的应用、方程组的解法等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题. |