9.用待定系数法求二次函数的解析式

 (1)一般式：.已知图像上三点或三对、的值，通常选择一般式.

 (2)顶点式：.已知图像的顶点或对称轴，通常选择顶点式.

 (3)交点式：已知图像与轴的交点坐标、，通常选用交点式：.

10.直线与抛物线的交点（或称二次函数与一次函数关系）

 (1)轴与抛物线得交点为()

 (2)与轴平行的直线与抛物线有且只有一个交点(,).

 (3)抛物线与轴的交点

二次函数的图像与轴的两个交点的横坐标、，是对应一元二次方程

的两个实数根.抛物线与轴的交点情况可以由对应的一元二次方程的根的判别式判定：

①有两个交点抛物线与轴相交；

②有一个交点(顶点在轴上)抛物线与轴相切；

③没有交点抛物线与轴相离.

(4)平行于轴的直线与抛物线的交点

同(3)一样可能有0个交点、1个交点、2个交点.当有2个交点时，两交点的纵坐标相等，设纵坐标为，则横坐标是的两个实数根.而根的存在情况仍如(3)一样由根的判别式判定。

(5)一次函数的图像与二次函数的图像的交点，由方程组

的解的数目来确定：

①方程组有两组不同的解时与有两个交点; 

②方程组只有一组解时与只有一个交点；③方程组无解时与没有交点.

(6)抛物线与轴两交点之间的距离：若抛物线与轴两交点为，由于、是方程的两个根，故由韦达定理知：

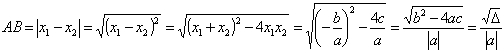
11．二次函数与一元二次方程的关系：

(1)一元二次方程就是二次函数当函数y的值为0时的情况．

(2)二次函数的图象与轴的交点有三种情况：有两个交点、有一个交点、没有交点；当二次函数的图象与轴有交点时，交点的横坐标就是当时自变量的值，即一元二次方程的根．

(3)当二次函数的图象与轴有两个交点时，则一元二次方程有两个不相等的实数根；当二次函数的图象与轴有一个交点时，则一元二次方程有两个相等的实数根；当二次函数的图象与轴没有交点时，则一元二次方程没有实数根

12.二次函数的应用：

(1)二次函数常用来解决最优化问题，这类问题实际上就是求函数的****(小)值。一般而言，****(小)值会在顶点处取得，达到****(小)值时的即为顶点横坐标值，****(小)值也就是顶点纵坐标值。

(2)二次函数的应用包括以下方面：分析和表示不同背景下实际问题中变量之间的二次函数关系；

运用二次函数的知识解决实际问题中的****(小)值．