1.(4分)(2013秋•宿迁期中)函数y=x﹣2在区间的****值是 .
2.(4分)函数y=x3和y=![]() 的图象关于直线 对称.
的图象关于直线 对称.
3.(4分)关于幂函数y=xα,下列命题正确的是序号是 .
①当α=0时,图象是一条直线; ②图象都过点(0,0)和(1,1);
③若是奇函数,则一定是增函数; ④图象不可能出现在第四象限.
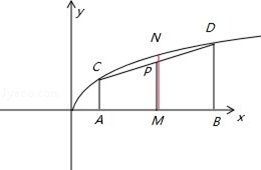
4.(4分)幂函数f(x)=![]() ,若0<x1<x2,则
,若0<x1<x2,则![]() 与
与![]() 中较大者为 .
中较大者为 .
5.(4分)(2013秋•海原县校级期末)函数y=![]() 的定义域为 .
的定义域为 .
6.(4分)(2007•长宁区一模)若函数f(x)=2﹣|x﹣1|﹣m的图象与x轴有交点,则实数m的取值范围是 .
7.(4分)(2010秋•沧浪区校级月考)函数y=x﹣2的值域是 .
8.(4分)a=![]() 与b=
与b=![]() 的大小关系是 .
的大小关系是 .
9.(4分)(2006•辽宁)设函数![]() ,则
,则![]() = .
= .
10.(4分)0<x<y<1,则下列不等式中正确的序号为 .
①3y<3x;②logx3<logy3;③log4x<log4y; ④![]() <
<![]() .
.
1.(4分)(2013秋•宿迁期中)函数y=x﹣2在区间的****值是 4 . 考点: 幂函数的概念、解析式、定义域、值域.菁优网版权所有 专题: 计算题. 分析: 根据幂函数当a>0时,则函数y=xa在区间(0,+∞)上单调递增,当a<0时,则函数y=xa在区间(0,+∞)上单调递减,我们易判断函数y=x﹣2在区间上的单调性,进而得到函数y=x﹣2在区间的****值. 解答: 解:根据幂函数的性质, ∵﹣2<0 ∴函数y=x﹣2在区间上单调递减 当x= 故答案为:4 点评: 本题考查的知识点是幂函数的性质,根据指数a的值判断函数的单调性是解答本题的关键. 2.(4分)函数y=x3和y= 考点: 奇偶函数图象的对称性.菁优网版权所有 专题: 阅读型. 分析: 因为y= 解答: 解:由y= 根据反函数图象的性质可知函数y=x3和y= 故答案为y=x 点评: 考查学生掌握互为反函数的两个函数间的关系及图象关于直线y=x对称的性质.考查类比猜测,合情推理的探究能力和创新精神. 3.(4分)关于幂函数y=xα,下列命题正确的是序号是 ④ . ①当α=0时,图象是一条直线; ②图象都过点(0,0)和(1,1); ③若是奇函数,则一定是增函数; ④图象不可能出现在第四象限. 考点: 幂函数的性质.菁优网版权所有 专题: 综合题. 分析: 通过求函数的定义域,判断出①错;通过举反例说明②③错;通过求点的坐标的范围判断出④对. 解答: 对于①,当α=0时,幂函数的定义域为x≠0,所以图象是去掉点(0,1)的一条直线,故①错 对于②,例如幂函数y=x﹣1,图象不过(0,0),故②错 对于③,例如幂函数y=x﹣1是奇函数,但不是增函数,故③错 对于④,因为x>0时,y=xα>0,故幂函数图象不可能出现在第四象限,故④对 故答案为:④ 点评: 本题考查幂函数的性质:定义域、过定点、单调性、奇偶性. 4.(4分)幂函数f(x)= 考点: 幂函数的性质.菁优网版权所有 专题: 计算题;作图题;数形结合. 分析: 画出幂函数的图象,x>0 时函数是凸函数,可得 解答: 解:作出幂函数x>0时的图象,如图: 由题意不妨A(x1,0)B(x2,0) 函数是凸函数, 所以:MP= 显然: 故答案为: 点评: 本题考查幂函数的性质,考查作图能力,判断能力,是基础题. 5.(4分)(2013秋•海原县校级期末)函数y= 考点: 函数的定义域及其求法.菁优网版权所有 专题: 计算题. 分析: 欲求函数的定义域,即须被开方数要是非负数即可,即 解答: 解:由 x ∴函数y= 故答案为:{x|x 点评: 本题主要考查了函数的定义域及其求法,以及利用指数函数的性质求解不等式,属于基础题. 6.(4分)(2007•长宁区一模)若函数f(x)=2﹣|x﹣1|﹣m的图象与x轴有交点,则实数m的取值范围是 0<m≤1 . 考点: 指数函数的图像与性质;指数函数综合题.菁优网版权所有 专题: 转化思想. 分析: 题目中条件:“函数f(x)=2﹣|x﹣1|﹣m的图象与x轴有交点,”转化成函数m=2﹣|x﹣1|的图象与x轴有交点,即函数的值域问题求解. 解答: 解:∵函数f(x)=2﹣|x﹣1|﹣m的图象与x轴有交点, ∴函数m=2﹣|x﹣1|的图象与x轴有交点, ∴即函数m=2﹣|x﹣1|的值域问题. ∴m=2﹣|x﹣1|的∈(0,1]. 故填:0<m≤1. 点评: 本题考查函数与方程思想在求解范围问题中的应用,函数与方程中蕴涵着丰富的数学思想方法,在解有关函数与方程问题时,应注意数学思想方法的挖掘、提炼、总结,以增强分析问题和解决问题的能力 7.(4分)(2010, 秋•沧浪区校级月考)函数y=x﹣2的值域是 (0,+∞) . 考点: 函数的值域.菁优网版权所有 专题: 计算题. 分析: 先求函数的定义域,然后结合二次函数的值域求解即可 解答: 解:由题意可得函数的定义域x≠0 ∴x2>0 ∴ 故答案为:(0,+∞) 点评: 本题主要考查二次函数的值域,属于求二次函数的最值问题,属于基本题. 8.(4分)a= 考点: 幂函数的性质.菁优网版权所有 专题: 计算题. 分析: 构造函数;利用幂函数的指数的值,判断出函数的奇偶性、单调性,比较出a,b的大小. 解答: 解:考察函数y= 其定义域为R,为奇函数 ∵ ∴函数单调递增 ∵﹣0..88>﹣0.89 ∴a>b 故答案为a>b 点评: 本题考查幂函数的奇偶性、单调性都与幂函数的指数有关. 9.(4分)(2006•辽宁)设函数 考点: 函数的值域.菁优网版权所有 分析: 分段函数的求值问题,要注意自变量范围不同函数解析式就不同. 解答: 解: 故答案为: 点评: 本题考查了分段函数的运算法则以及指对数式的运算.注意:自变量范围的不同所对的函数式也不同. 10.(4分)0<x<y<1,则下列不等式中正确的序号为 ③ . ①3y<3x;②logx3<logy3;③log4x<log4y; ④ 考点: 对数函数的单调性与特殊点;指数函数的单调性与特殊点.菁优网版权所有 分析: ①根据指数函数y=3x是增函数,可知结论错;②利用对数的换底公式logx3= 解答: 解:∵0<x<y<1, ∴①根据指数函数y=3x是增函数,可知3y>3x;故①不正确; ②∵logx3= ∴ ③根据对数函数y=log4x在(0,+∞)上单调递增,log4x<log4y;故正确; ④根据指数函数y= 故答案③ 点评: 此题是个基础题.考查对数函数和指数函数的单调性,并利用单调性比较大小,考查学生灵活应用知识分析解决问题的能力.
![]() 时,函数y=x﹣2取****值4
时,函数y=x﹣2取****值4
![]() 的图象关于直线 y=x 对称.
的图象关于直线 y=x 对称.
![]() 得到x=y3,所以函数y=x3和y=
得到x=y3,所以函数y=x3和y=![]() 互为反函数关系,所以关于y=x对称.
互为反函数关系,所以关于y=x对称.
![]() 得到x=y3,所以这两个函数互为反函数,
得到x=y3,所以这两个函数互为反函数,![]() 的图象关于直线 y=x对称.
的图象关于直线 y=x对称.
![]() ,若0<x1<x2,则
,若0<x1<x2,则![]() 与
与![]() 中较大者为
中较大者为 ![]() .
.
![]() 与
与![]() 中较大者.
中较大者.
![]() ;MN=
;MN=![]()
![]()
![]()
![]() 的定义域为 {x|x
的定义域为 {x|x![]() } .
} .
![]() ,由此即得所求的定义域.
,由此即得所求的定义域.
![]() 得:
得:![]() ,
,![]() 的定义域为{x|x
的定义域为{x|x![]() },
},![]() }.
}.
![]()
![]() 与b=
与b=![]() 的大小关系是 a>b .
的大小关系是 a>b .
![]()
![]()
![]() ,则
,则![]() =
= ![]() .
.
![]()
![]() .
.
![]() <
<![]() .
.
![]() ,logy3=
,logy3=![]() 和对数函数的单调性可知,②错;③根据对数函数y=log4x在(0,+∞)上单调递增,可知结论正确;④根据指数函数y=
和对数函数的单调性可知,②错;③根据对数函数y=log4x在(0,+∞)上单调递增,可知结论正确;④根据指数函数y=![]() 是减函数,可知结论错.从而得到答案.
是减函数,可知结论错.从而得到答案.
![]() ,logy3=
,logy3=![]() ,根据对数函数y=log3x在(0,+∞)上单调递增,得log3x<log3y<0,
,根据对数函数y=log3x在(0,+∞)上单调递增,得log3x<log3y<0,![]() ,即logx3>logy3,故②错;
,即logx3>logy3,故②错;![]() 是减函数,得
是减函数,得![]() ,故④错,
,故④错,