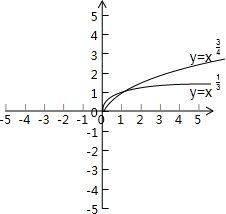
11.求证幂函数y=x3是R上的奇函数且为增函数.
12.作函数f(x)=|log3x|的图象,并求f(x)>f(2)的x的范围.
13.幂函数f(x)与g(x)分别过点(3,![]() )、(﹣8,﹣2)
)、(﹣8,﹣2)
(1)求此两个函数的解析式;
(2)判断两个函数的奇偶性;
(3)求函数f(x)<g(x)的解集.
14.幂函数f(x)=xn(n∈Z)具有性质f2(1)+f2(﹣1)=2,判断函数f(x)的奇偶性.
11.求证幂函数y=x3是R上的奇函数且为增函数. 考点: 幂函数的性质;函数单调性的判断与证明;函数奇偶性的判断.菁优网版权所有 专题: 综合题. 分析: 将函数中的x换为﹣x,判断f(﹣x)与f(x)的关系证出奇函数;求出导函数,判断导函数的符号,判断出递增函数. 解答: 证明:设f(x)=x3 ∴f(﹣x)=(﹣x)3=﹣x3=﹣f(x) ∴f(x)是奇函数, 对于f(x)=x3,其定义域为R, 设x1<x2, 则f(x1)﹣f(x2)=x13﹣x23=(x1﹣x2)(x12+x1x2+x22)<0; ∴f(x)在R是递增函数 ∴幂函数y=x3是R上的奇函数且为增函数 点评: 本题考查奇函数的定义、考查利用导函数的符号判断函数的单调性. 12.作函数f(x)=|log3x|的图象,并求f(x)>f(2)的x的范围. 考点: 对数函数的图像与性质.菁优网版权所有 专题: 计算题;作图题. 分析: 因为f(x)=|log3x|= 解答: 解:因为f(x)=|log3x|= 图象如图所示: f(x)>f(2)⇔|log3x|>log32 ⇔log3x>log32或log3x<﹣log32 ⇔x>2或0<x< 点评: 本题考查含有****值函数的图象的做法、函数的对称变换、解不等式等知识. 13.幂函数f(x)与g(x)分别过点(3, (1)求此两个函数的解析式; (2)判断两个函数的奇偶性; (3)求函数f(x)<g(x)的解集. 考点: 幂函数的性质;函数解析式的求解及常用方法;函数奇偶性的判断.菁优网版权所有 专题: 计算题;数形结合;待定系数法. 分析: (1)设出函数表达式,代入点的坐标,即可求出两个函数的解析式; (2)求出f(x)的定义域,判断函数f(x)的奇偶性;g(x)的奇偶性容易得到. (3)求出函数f(x)<g(x)的表达式,结合幂函数f(x)与g(x)的图象,求函数f(x)<g(x)的解集. 解答: 解:(1)设幂函数f(x)=xa与g(x)=xb; 幂函数f(x)与g(x)分别过点(3, 所以: ∴a= ∴两个函数的解析式:f(x)= (2)f(x)= 所以它是非奇非偶函数;g(x)= 所以是奇函数; (3)因为函数f(x)<g(x),所以 当1>x>0时, 当x>1时, 所以不等式的解集为:{x|1>x>0} 点评: 本题考查幂函数的性质,待定系数法求函数解析式,函数奇偶性的判断,考查计算能力,是基础题. 14.幂函数f(x)=xn(n∈Z)具有性质f2(1)+f2(﹣1)=2,判断函数f(x)的奇偶性. 考点: 函数奇偶性的判断;幂函数的性质.菁优网版权所有 专题: 证明题. 分析: 先化简题目中的等式,分n为奇数和n为偶数2种情况讨论,最后确定n一定为偶数,从而得出幂函数f(x)=xn(n∈Z)是个偶函数. 解答: 解:由题意得:(1n)2+((﹣1)n)2=2,2=2①, 当n为奇数时,①不成立,当n为偶数时,①恒成立,故n一定为偶数, ∴幂函数f(x)=xn(n∈Z)是个偶函数. 点评: 本题考查幂函数的性质、以及函数奇偶性的判断.
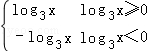 ,故只需作出y=log3x的图象,保留x轴上方的部分不变,将x轴下方的部分做关于x轴的对称图象即可.由图象可对f(x)>f(2)直接求解.
,故只需作出y=log3x的图象,保留x轴上方的部分不变,将x轴下方的部分做关于x轴的对称图象即可.由图象可对f(x)>f(2)直接求解.
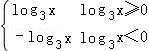 ,
,![]()
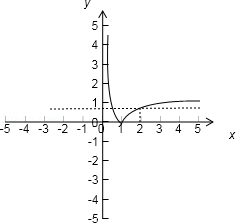
![]() )、(﹣8,﹣2)
)、(﹣8,﹣2)
![]() )、(﹣8,﹣2)
)、(﹣8,﹣2)![]() =3a,﹣2=(﹣8)b;
=3a,﹣2=(﹣8)b;![]() ,b=
,b=![]()
![]() 与g(x)=
与g(x)=![]() ;
;![]() 的定义域是x≥0,
的定义域是x≥0,![]() 因为g(﹣x)=﹣g(x),
因为g(﹣x)=﹣g(x),![]() (x≥0)
(x≥0)![]() 成立;
成立;![]() 不成立;
不成立;