1.不等式(x-1)(2-x)≥0的解集为(　　)

A.{x|1≤x≤2}            B.{x|x≤1或x≥2}

C.{x|1<x<2}               D.{x|x<1或x>2}

【解析】选A.因为(x-1)(2-x)≥0,

所以(x-2)(x-1)≤0,

所以结合二次函数的性质可得1≤x≤2.

故选A.

2.(2015·成都模拟)使不等式2x²-5x-3≥0成立的一个充分不必要条件是(　　)

A.x≥0                 B.x<0或x>2

C.x∈{-1,3,5}         D.x≤-或x≥3

【解析】选C.不等式2x²-5x-3≥0的解集是.

由题意,选项中x的范围应该是上述解集的真子集,只有C满足.

3.(2015·潍坊模拟)函数f(x)=的定义域是(　　)

A.(-∞,1)∪(3,+∞)          B.(1,3)

C.(-∞,2)∪(2,+∞)          D.(1,2)∪(2,3)

【解析】选D.由题意知

即

故函数f(x)的定义域为(1,2)∪(2,3).

【加固训练】不等式≤0的解集为(　　)

A.

B.

C.∪

A.{x|x<-1或x>lg2}        B.{x|-1<x<lg2}

C.{x|x>-lg2}             D.{x|x<-lg2}

【解析】选C.由题意,得10^x<-1,或10^x>,

10^x<-1无解;

由10^x>,得x>lg,即x>-lg2.

5.(2015·杭州模拟)若x=1满足不等式ax²+2x+1<0,则实数a的取值范围是(　　)

A.(-∞,-3)               B.(-3,+∞)

C.(1,+∞)                D.(-∞,1)

【解析】选A.因为x=1满足不等式ax²+2x+1<0,

所以a+2+1<0,

所以a<-3.故选A.

6.关于x的不等式x²-ax+a>0(a∈R)在R上恒成立的充分不必要条件是(　　)

A.a<0或a>4               B.0<a<2

C.0<a<4                  D.0<a<8

【解析】选B.本题考查一元二次不等式的解法及充分必要条件的判断.由x²-ax+a>0(a∈R)在R上恒成立可知,Δ=a²-4a<0,所以0<a<4.当0<a<2时,Δ=a²-4a<0,x²-ax+a>0(a∈R)在R上恒成立;反之不成立.故其充分不必要条件为0<a<2.

7.已知函数f(x)=ax²-x-c,且不等式ax²-x-c>0的解集为{x|-2<x<1},则函数y=f(-x)的图象为(　　)

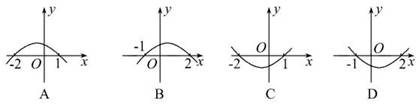
【解析】选B.因为函数f(x)=ax²-x-c,

且不等式ax²-x-c>0的解集为{x|-2<x<1},

所以a<0,方程ax²-x-c=0的两个根为-2和1,

-2+1=,-2×1=-,

所以a=-1,c=-2,

所以f(x)=ax²-x-c=-x²-x+2,

所以f(-x)=-x²+x+2,其图象开口向下,与x轴交点为(-1,0),(2,0),故选B.

二、填空题(每小题5分,共15分)

8.已知函数f(x)=若f(f(1))>3a²,则a的取值范围是　　　　.

【解析】f(1)=2¹+1=3,所以f(f(1))=f(3)=9+6a.

由f(f(1))>3a²得9+6a>3a²,

即a²-2a-3<0,解得-1<a<3.

答案:(-1,3)

【误区警示】此题是分段函数,代入求值时容易出现因不同的取值而出现错误,应注意分段函数分段求值,不能代错.

9.(2015·北京模拟)已知p:x≥k,q:<1,若p是q的充分不必要条件,则实数

k的取值范围是　　　　.

【解题提示】先解出分式不等式的解集,再利用p是q的充分不必要条件,可得结果.

【解析】<1⇔>0⇔x∈(-∞,-1)∪(2,+∞),k∈(2,+∞).

答案:k∈(2,+∞)

10.当x∈(1,2)时,不等式x²+mx+4<0恒成立,则m的取值范围是　　　　　　.

【解析】当x∈(1,2)时,不等式x²+mx+4<0恒成立⇒m<-=-在x∈(1,2)上恒成立,设φ(x)=-,φ(x)=-∈(-5,-4),故m≤-5.

所以m的取值范围为(-∞,-5].

答案:(-∞,-5]

【一题多解】本题还有以下解法

设f(x)=x²+mx+4,因为当x∈(1,2)时,不等式x²+mx+4<0恒成立,又因为f(0)=4,f(x)开口向上,所以若f(x)<0在(1,2)恒成立,则: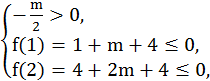解得m≤-5.

所以m的取值范围为(-∞,-5].

答案:(-∞,-5]