一、选择题(本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的)

1．已知集合M＝{x∈R|y＝lg(2－x)}，N＝{y∈R|y＝2^x－1}，则(　　)

A．M＝N   B．M∩N＝∅

C．M⊇N   D．M∪N＝R

2．(2015·广东阳东一中联考)函数f(x)＝1－x(1)＋lg(1＋x)的定义域是(　　)

A．(－∞，－1)   B．(1，＋∞)

C．(－1,1)∪(1，＋∞)   D．(－∞，＋∞)

3．(2015·浙江嘉兴桐乡第一中学新高考调研(二))若a∈R，则“a＝1”是“|a|＝1”的(　　)

A．充分不必要条件 B．必要不充分条件

C．充要条件 D．既不充分也不必要条件

4．(2015·皖南八校第三次联考)已知命题p：∀x∈R,2^x>x²；命题q：∃x∈(－2，＋∞)，使得(x＋1)·e^x≤1，则下列命题中为真命题的是(　　)

A．p∧q   B．p∨(綈q)

C．(綈p)∧q   D．(綈p)∧(綈q)

5．若函数f(x)＝|2x＋a|的单调递增区间是[3，＋∞)，则a等于(　　)

A．6   B．－6

C．0   D．12

6．(2015·呼伦贝尔二模)已知函数f(x)＝ex，x>0，(0，x≤0，)则使函数g(x)＝f(x)＋x－m有零点的实数m的取值范围是(　　)

A．[0,1)   B．(－∞，1)

C．(－∞，0]∪(1，＋∞)   D．(－∞，1]∪(2，＋∞)

7．(2015·安徽江淮名校第二次联考)已知函数f(x)对定义域R内的任意x都有f(2＋x)＝f(6－x)，且当x≠4时其导函数f′(x)满足xf′(x)>4f′(x)．若9<a<27，则(　　)

A．f(2)<f(6)<f(log₃a) B．f(6)<f(2)<f(log₃a)

C．f(log₃a)<f(2)<f(6) D．f(log₃a)<f(6)<f(2)

8．已知函数f(x)＝－x2＋1＋a，x≥0，(－x2－2x＋a，x<0，)且函数y＝f(x)－x恰有3个不同的零点，则实数a的取值范围是(　　)

A．(0，＋∞)   B．[－1,0)

C．[－1，＋∞)   D．[－2，＋∞)

第Ⅱ卷

二、填空题(本大题共6小题，每小题5分，共30分．把答案填在题中横线上)

9．已知命题p：－4<x－a<4，命题q：(x－2)(3－x)>0，若綈p是綈q的充分条件，则实数a的取值范围是________．

10．若函数f(x)＝log_0.5(3x²－ax＋5)在(－1，＋∞)上是减函数，则实数a的取值范围是__________．

11．若函数f(x)是周期为4的奇函数，且在[0,2]上的解析式为f(x)＝sin πx，1<x≤2，(x(1－x)，0≤x≤1，)则f(4(29))＋f(6(41))＝________.

12．(2015·江苏时杨中学月考)已知m≠0，函数f(x)＝－x－2m，x>2，(3x－m，x≤2，)若f(2－m)＝f(2＋m)，则实数m的值为________．

13．(2015·北京)设函数f(x)＝4(x－a)(x－2a)，x≥1.(2x－a，x＜1，)

(1)若a＝1，则f(x)的最小值为________；

(2)若f(x)恰有2个零点，则实数a的取值范围是___________________________________．

14．(2015·湖北浠水实验高中上学期期中)某商店计划投入资金20万元经销甲或乙两种商品，已知经销甲、乙商品所获利润分别为P和Q(万元)，且它们与投入资金x(万元)的关系是P＝4(x)，Q＝2(a)(a>0)，若不管资金如何投放，经销这两种商品或其中一种商品所获利润总不小于5万元，则a的最小值为________．

三、解答题(本大题共6小题，共80分．解答应写出文字说明、证明过程或演算步骤)

15．(13分)(2015·珠海六校第二次联考)已知集合A＝{x||x－a|≤2}，B＝{x|lg(x²＋6x＋9)>0}．

(1)求集合A和∁_RB；

(2)若A⊆B，求实数a的取值范围．

16．(13分)(2015·福建八县(市)一中联考)设p：实数x满足x²－4ax＋3a²<0(其中a≠0)，q：实数x满足x－2(x－3)<0.

(1)若a＝1，且p∧q为真，求实数x的取值范围；

(2)若p是q的必要不充分条件，求实数a的取值范围．

17.(13分)(2015·德州第一中学月考)已知函数f(x)的定义域为(－2,2)，函数g(x)＝f(x－1)＋f(3－2x)．

(1)求函数g(x)的定义域；

(2)若f(x)是奇函数，且在定义域上单调递减，求不等式g(x)≤0的解集．

18．(13分)(2015·福州上学期期末质量检测)函数f(x)＝x²－mx (m>0)在区间[0,2]上的最小值记为g(m)．

(1)若0<m≤4，求函数g(m)的解析式；

(2)定义在(－∞，0)∪(0，＋∞)的函数h(x)为偶函数，且当x>0时，h(x)＝g(x)．若h(t)>h(4)，求实数t的取值范围．

19.(14分)经市场调查，某旅游城市在过去的一个月内(以30天计)，旅游人数f(t)(万人)与时间t(天)的函数关系近似地满足f(t)＝4＋t(1)，人均消费g(t)(元)与时间t(天)的函数关系近似地满足g(t)＝115－|t－15|.

(1)求该城市的旅游日收益ω(t)(万元)与时间t(1≤t≤30，t∈N)的函数关系式；

(2)求该城市的旅游日收益的最小值．

20．(14分)已知定义域为R的函数f(x)＝2x＋1＋2(－2x＋b)是奇函数．

(1)求b的值；

(2)判断函数f(x)的单调性并证明；

(3)若对任意的t∈R，不等式f(t²－2t)＋f(2t²－k)<0恒成立，求k的取值范围．

答案解析

1．D　[集合M是函数y＝lg(2－x)的定义域，所以M＝(－∞，2)，集合N为函数y＝2^x－1的值域，所以N＝(0，＋∞)，所以M∪N＝R.]

2．C　[∵1＋x>0，(1－x≠0，)∴x>－1且x≠1，

所以C为正确选项，故选C.]

3．A　[“若a＝1，则|a|＝1”是真命题，即a＝1⇒|a|＝1，由|a|＝1可得a＝±1，所以“若|a|＝1，则a＝1”是假命题，即|a|＝1D⇒/a＝1.所以“a＝1”是“|a|＝1”的充分不必要条件．故选A.]

4．C　[对于命题p：当x＝2时，2^x＝x²，∴命题p是假命题，綈p是真命题；对于命题q：当x＝0时，(x＋1)·e^x＝1，所以命题q是真命题，逐项检验可知，只有(綈p)∧q是真命题，故选C.]

5．B　[作出函数f(x)的图象，

可知函数f(x)在(－∞，－2(a)]上单调递减，

在[－2(a)，＋∞)上单调递增．

又已知函数f(x)的单调递增区间是[3，＋∞)，

所以－2(a)＝3，解得a＝－6.]

6．C　[设函数h(x)＝f(x)＋x，当x≤0时，h(x)＝x是增函数，此时h(x)的值域是(－∞，0]；

当x>0时，h(x)＝e^x＋x是增函数，此时h(x)的值域是(1，＋∞)．

综上，h(x)的值域是(－∞，0]∪(1，＋∞)．

函数g(x)＝f(x)＋x－m有零点，即方程f(x)＋x－m＝0有解，也即方程m＝f(x)＋x有解．故m的取值范围是(－∞，0]∪(1，＋∞)．]

7．D　[由f(2＋x)＝f(6－x)知函数f(x)图象关于直线x＝4对称，又∵xf′(x)>4f′(x)，∴(x－4)f′(x)>0.

∴函数f(x)在(－∞，4)上是减函数，在(4，＋∞)上是增函数．又∵9<a<27，∴2<log_{3a<3，∴f(log3a)<f(2)＝f(6)．又∵9<a<27，∴3<<3，∴2>2³＝8.}

∴f(2)>f(8)>f(6)>f(log₃a)，故选D.]

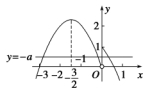
8．B　[函数y＝f(x)－x恰有3个不同的零点等价于函数y＝－x2－x＋1，x≥0(－x2－3x，x<0，)的图象与直线y＝－a有3个不同的交点，作出图象，如图所示，可得当0<－a≤1时，满足题意，故－1≤a<0.故选B.]

9．[－1,6]

解析　由p：－4<x－a<4成立，得a－4<x<a＋4；

由q：(x－2)(3－x)>0成立，得2<x<3，

所以綈p：x≤a－4或x≥a＋4，綈q：x≤2或x≥3，

又綈p是綈q的充分条件，所以a＋4≥3，(a－4≤2，)解得－1≤a≤6，故答案为[－1,6]．

10．[－8，－6]

解析　设g(x)＝3x²－ax＋5，由已知得g(－1)≥0，(≤－1，)

解得－8≤a≤－6.

11.16(5)

解析　因为函数f(x)的周期是4，

则f(4(29))＝f(8－4(3))＝f(－4(3))，

∵f(x)是奇函数，

∴f(－4(3))＝－f(4(3))＝－4(3)×4(1)＝－16(3)，

f(6(41))＝f(8－6(7))＝f(－6(7))＝－f(6(7))＝－sin6(7π)

＝sin6(π)＝2(1)，

则f(4(29))＋f(6(41))＝－16(3)＋2(1)＝16(5).

12．8或－3(8)

解析　若m>0，则f(2－m)＝3(2－m)－m＝6－4m，

f(2＋m)＝－(2＋m)－2m＝－2－3m，∴6－4m＝－2－3m，解得m＝8.若m<0，则f(2－m)＝－(2－m)－2m＝－2－m，f(2＋m)＝3(2＋m)－m＝6＋2m，∴－2－m＝6＋2m，解得m＝－3(8).

13．(1)－1　(2)，1(1)∪[2，＋∞)

解析　(1)当a＝1时，f(x)＝4(x－1)(x－2)，x≥1.(2x－1，x<1，)

当x<1时，f(x)＝2^x－1∈(－1,1)，

当x≥1时，f(x)＝4(x²－3x＋2)

＝44(1)≥－1，

∴f(x)_min＝－1.

(2)由于f(x)恰有2个零点，分两种情况讨论：

当f(x)＝2^x－a，x<1没有零点时，a≥2或a≤0.

当a≥2时，f(x)＝4(x－a)(x－2a)，x≥1时，有2个零点；

当a≤0时，f(x)＝4(x－a)(x－2a)，x≥1时无零点．

因此a≥2满足题意．

当f(x)＝2^x－a，x<1有一个零点时， 0<a<2.

f(x)＝4(x－a)(x－2a)，x≥1有一个零点，此时a<1, 2a≥1，因此2(1)≤a<1.

综上知实数a的取值范围是≤a<1或a≥2(1).

14.

解析　设经销乙商品投入资金x万元，由题意得

4(20－x)＋2(a)≥5(0≤x≤20)，整理得－4(x)＋2(a)≥0.显然，当x＝0时，不等式恒成立；当0<x≤20时，由－4(x)＋2(a)≥0，得a≥2(x)恒成立．因为当0<x≤20时，0<2(x)≤，所以a≥，即a的最小值为.

15．解　(1)∵|x－a|≤2⇔－2≤x－a≤2⇔a－2≤x≤2＋a，

∴集合A＝{x|－2＋a≤x≤2＋a}，

∵lg(x²＋6x＋9)>0，

∴x²＋6x＋9>1，∴集合B＝{x|x<－4或x>－2}．

∴∁_RB＝[－4，－2]．

(2)由A⊆B，得2＋a<－4或者－2<－2＋a.

解得a<－6或a>0，

所以a的取值范围为{a|a<－6或a>0}．

16．解　(1)当a＝1时，由x²－4ax＋3a²<0，解得1<x<3，即p为真时，实数x的取值范围是(1,3)；由x－2(x－3)<0，解得2<x<3，即q为真时，实数x的取值范围是(2,3)．若p∧q为真，则p为真且q为真，所以实数x的取值范围是(2,3)．

(2)由x²－4ax＋3a²<0，得(x－3a)(x－a)<0.

当a>0时，p：a<x<3a，所以3a≥3，(a≤2，)解得1≤a≤2；

当a<0时，p：3a<x<a，而a≥3(3a≤2，)无解，不合题意．

所以实数a的取值范围是[1,2]．

17．解　(1)由题意可知－2<3－2x<2，(－2<x－1<2，)

解得2(1)<x<2(5)，

∴函数g(x)的定义域为(2(1)，2(5))．

(2)由g(x)≤0得f(x－1)＋f(3－2x)≤0，

∴f(x－1)≤－f(3－2x)．

∵f(x)是奇函数，∴f(x－1)≤f(2x－3)．

又∵f(x)在(－2,2)上单调递减，

∴x－1≥2x－3.(－2<2x－3<2，)

解得2(1)<x≤2，∴g(x)≤0的解集为(2(1)，2]．

18．解　(1)因为f(x)＝x²－mx＝2(m)²－4(m2)，

因为设f(x)在区间[0,2]上的最小值记为g(m)．

当0<m≤4时，0<2(m)≤2，

所以g(m)＝f2(m)＝－4(m2).

(2)当m>4时，f(x)＝2(m)²－4(m2)在[0,2]上单调递减，

所以g(m)＝f(2)＝4－2m.

结合(1)可知，g(m)＝4－2m，m>4.(，0<m≤4，)

因为x>0时，h(x)＝g(x)，

所以x>0时，h(x)＝4－2x，x>4.(，0<x≤4，)

易知函数h(x)在(0，＋∞)上单调递减，

因为定义在(－∞，0)∪(0，＋∞)的函数h(x)为偶函数，且h(t)>h(4)，

所以h(|t|)>h(4)，所以0<|t|<4，

所以|t|<4，(t≠0，)即－4<t<4，(t≠0，)

从而－4<t<0或0<t<4.

综上所述，所求实数t的取值范围为(－4,0)∪(0,4)．

19．解　(1)由题意得，ω(t)＝f(t)·g(t)＝(4＋t(1))(115－|t－15|)(1≤t≤30，t∈N)，

即ω(t)＝)(130－t)(15≤t≤30，t∈N).(1)

(2)①当1≤t<15，t∈N时，ω(t)＝(4＋t(1))(t＋100)

＝4(t＋t(25))＋401≥4×2＋401＝441，当且仅当t＝t(25)，即t＝5时取等号，此时ω(t)取最小值，为441；

②当15≤t≤30，t∈N时，ω(t)＝(4＋t(1))(130－t)＝519＋(t(130)－4t)，易知ω(t)在[15,30]上单调递减，所以当t＝30时，ω(t)取最小值，为4033(1).

因为4033(1)<441，所以该城市旅游日收益的最小值为4033(1)万元．

20．解　(1)∵f(x)在定义域R上是奇函数，

∴f(0)＝0，即2＋2(b－1)＝0，∴b＝1.

(2)由(1)知f(x)＝2＋2x＋1(1－2x)＝－2(1)＋2x＋1(1).

设x₁<x₂，则f(x₁)－f(x₂)＝2x1＋1(1)－2x2＋1(1)

＝(2x1＋1)(2x2＋1)(2x2－2x1).

∵函数y＝2^x在R上是增函数且x<, /I>₁<x₂，

∴2x₂－2x₁>0.

又(2x₁＋1)(2x₂＋1)>0，

∴f(x₁)－f(x₂)>0，即f(x₁)>f(x₂)，

∴f(x)在(－∞，＋∞)上为减函数．

(3)∵f(x)是奇函数，∴不等式f(t²－2t)＋f(2t²－k)<0等价于f(t²－2t)<－f(2t²－k)＝f(k－2t²)，

∵f(x)为减函数，由上式推得t²－2t>k－2t².

即对一切t∈R,3t²－2t－k>0，从而判别式Δ＝4＋12k<0⇒k<－3(1).

∴k的取值范围是(－∞，－3(1))．