1.充分理解逻辑联结词的含义，注意和日常用语的区别；

2.对量词的练习要在“含一个量词”框架内进行，不要随意加深；

3.注意逻辑与其他知识的交汇．

 

1．充分条件、必要条件与充要条件

(1)“若p，则q”形式的命题为真时，记作p⇒q，称p是q的充分条件，q是p的充要条件．

(2)如果既有p⇒q，又有q⇒p，记作p⇔q，则p是q的充要条件，q也是p的充要条件．

p是q的充要条件又常说成q当且仅当p，或p与q等价．

2．命题的四种形式及真假关系

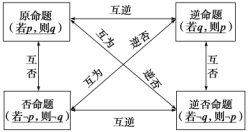
互为逆否的两个命题等价(同真或同假)；互逆或互否的两个命题不等价．

【特别提醒】等价命题和等价转化

(1)逆命题与否命题互为逆否命题；

(2)互为逆否命题的两个命题同真假；

(3)当判断原命题的真假比较困难时，可以转化为判断它的逆否命题的真假．

高频考点一　含有逻辑联结词的命题的真假判断

例1、(1)已知命题p：m，n为直线，α为平面，若m∥n，n⊂α，则m∥α，命题q：若a>b，则ac>bc，则下列命题为真命题的是(　　)

A．p∨q B．綈p∨q

C．綈p∧q D．p∧q

(2)已知命题p：若x>y，则－x<－y；命题q：若x>y，则x2>y2.在命题①p∧q；②p∨q；③p∧(綈q)；④(綈p)∨q中，真命题是(　　)

A．①③ B．①④

C．②③ D．②④

答案　(1)B　(2)C

【感悟提升】　“p∨q”“p∧q”“綈p”等形式命题真假的判断步骤：

(1)确定命题的构成形式；

(2)判断其中命题p、q的真假；

(3)确定“p∧q”“p∨q”“綈p”等形式命题的真假．

【变式探究】(1)已知命题p：对任意x∈R，总有2x>0；q：“x>1”是“x>2”的充分不必要条件，则下列命题为真命题的是(　　)

A．p∧q B．(綈p)∧(綈q)

C．(綈p)∧q D．p∧(綈q)

(2)若命题p：关于x的不等式ax＋b>0的解集是{x|x>－a(b)}，命题q：关于x的不等式(x－a)(x－b)<0的解集是{x|a<x<b}，则在命题“p∧q”、“p∨q”、“綈p”、“綈q”中，是真命题的有________．

答案　(1)D　(2)綈p、綈q

解析　(1)p为真命题，q为假命题，故綈p为假命题，綈q为真命题．从而p∧q为假，(綈p)∧(綈q)为假，(綈p)∧q为假，p∧(綈q)为真，故选D.

(2)依题意可知命题p和q都是假命题，所以“p∧q”为假、“p∨q”为假，“綈p”为真、“綈q”为真．

高频考点二、全称命题、特称命题的真假

例2、(1)下列命题中，为真命题的是(　　)

A．∀x∈R，x2>0 B．∀x∈R，－1<sinx<1

C．∃x0∈R,<0 D．∃x0∈R，tanx0＝2

(2)下列四个命题

p1：∃x0∈(0，＋∞)，2(1)<3(1)；

p2：∃x0∈(0,1)，logx0>logx0；

p3：∀x∈(0，＋∞)，2(1)x>logx；

p4：∀x∈3(1)，2(1)x<logx.

其中真命题是(　　)

A．p1，p3 B．p1，p4

C．p2，p3 D．p2，p4

答案　(1)D　(2)D

【变式探究】(1)命题“存在实数x，使x>1”的否定是(　　)

A．对任意实数x，都有x>1

B．不存在实数x，使x≤1

C．对任意实数x，都有x≤1

D．存在实数x，使x≤1

(2)设x∈Z，集合A是奇数集，集合B是偶数集．若命题p：∀x∈A,2x∈B，则綈p为：______________.

答案　(1)C　(2)∃x0∈A,2x0∉B

解析　(1)利用特称命题的否定是全称命题求解，“存在实数x，使x>1”的否定是“对任意实数x，都有x≤1”．故选C.