2016年高考题《不等式、推理与证明》专练
1.(2016年高考新课标Ⅰ卷理)设集合![]() ,
,![]() ,则
,则![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.(2016年高考新课标Ⅰ卷理)若![]() ,则
,则
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.(2016年高考浙江卷理) 在平面上,过点P作直线l的垂线所得的垂足称为点P在直线l上的投影.由区域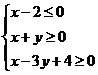 中的点在直线x+y
中的点在直线x+y![]() 2=0上的投影构成的线段记为AB,则|AB|=
2=0上的投影构成的线段记为AB,则|AB|=
A.2![]() B.4 C.3
B.4 C.3![]() D.
D.![]()
4.(2016年高考北京卷理)若![]() 满足
满足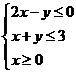 ,则
,则![]() 的****值为
的****值为
A.0 B.3 C.4 D.5
5.(2016年高考浙江卷理)已知实数a,b,c.
A.若|a2+b+c|+|a+b2+c|≤1,则a2+b2+c2<100 B.若|a2+b+c|+|a2+b–c|≤1,则a2+b2+c2<100
C.若|a+b+c2|+|a+b–c2|≤1,则a2+b2+c2<100 D.若|a2+b+c|+|a+b2–c|≤1,则a2+b2+c2<100
6.(2016年高考四川卷理)设p:实数x,y满足![]() ,q:实数x,y满足
,q:实数x,y满足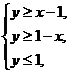 则p是q的
则p是q的
A.必要不充分条件 B.充分不必要条件
C.充要条件 D.既不充分也不必要条件
7.(2016年高考北京卷理)袋中装有偶数个球,其中红球、黑球各占一半.甲、乙、丙是三个空盒.每次从袋中任意取出两个球,将其中一个球放入甲盒,如果这个球是红球,就将另一个球放入乙盒,否则就放入丙盒.重复上述过程,直到袋中所有球都被放入盒中,则
A.乙盒中黑球不多于丙盒中黑球 B.乙盒中红球与丙盒中黑球一样多
C.乙盒中红球不多于丙盒中红球 D.乙盒中黑球与丙盒中红球一样多
8.(2016年高考山东卷理)若变量x,y满足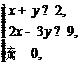 则
则![]() 的****值是
的****值是
A.4 B.9 C.10 D.12![]()
9.(2016年高考天津卷理)设变量x,y满足约束条件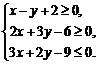 则目标函数
则目标函数![]() 的最小值为
的最小值为
A.![]() B.6 C.10 D.17
B.6 C.10 D.17
10.(2016年高考上海卷理)设x![]() ,则不等式
,则不等式![]() 的解集为__________.
的解集为__________.
11.(2016年高考江苏卷理)函数y=![]() 的定义域是 .
的定义域是 .
12.(2016年高考新课标Ⅲ卷理)若![]() 满足约束条件
满足约束条件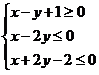 ,
,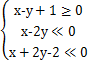
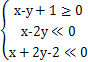 则
则![]() 的****值为_____________.
的****值为_____________.
13.(2016年高考江苏卷理)已知实数![]() 满足
满足 ,则
,则![]() 的取值范围是 .
的取值范围是 .
14.(2016年高考新课标Ⅰ卷理) 某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料1.5 kg,乙材料1 kg,用5个工时;生产一件产品B需要甲材料0.5 kg,乙材料0.3 kg,用3个工时,生产一件产品A的利润为2100元,生产一件产品B的利润为900元.该企业现有甲材料150 kg,乙材料90 kg,则在不超过600个工时的条件下,生产产品A、产品B的利润之和的****值为 元.
15.(2016年高考新课标Ⅱ卷理)有三张卡片,分别写有1和2,1和3,2和3.甲、乙、丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是 .
![]()
1.D 【解析】因为![]() 所以
所以![]()
![]() 故选D.
故选D.
2.C 【解析】用特殊值法,令![]() ,
,![]() ,
,![]() 得
得![]() ,选项A错误,
,选项A错误,![]() ,选项B错误,
,选项B错误,![]() ,选项C正确,
,选项C正确,![]() ,选项D错误,故选C.
,选项D错误,故选C.
【名师点睛】比较幂或对数值的大小时,若幂的底数相同或对数的底数相同,通常利用指数函数或对数函数的单调性进行比较;若底数不同,可考虑利用中间量进行比较.
3.C 【解析】如图,![]() 为不等式组所表示的平面区域,区域内的点在直线
为不等式组所表示的平面区域,区域内的点在直线![]() 上的投影构成了线段
上的投影构成了线段![]() ,即
,即![]() ,而
,而![]() ,由
,由![]() 得
得![]() ,由
,由![]() 得
得![]() ,所以
,所以![]() .故选C.
.故选C.
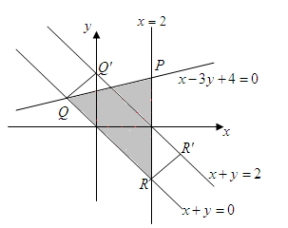
【思路点睛】先根据不等式组画出可行域,再根据题目中的定义确定![]() 的值.画不等式组所表示的平面区域时要注意通过特殊点验证,防止出现错误.
的值.画不等式组所表示的平面区域时要注意通过特殊点验证,防止出现错误.
4.C 【解析】作出约束条件表示的可行域,如图中阴影部分所示,则当![]() 经过点
经过点![]() 时,z取得****值,又
时,z取得****值,又![]() ,所以所求****值为4.
,所以所求****值为4.
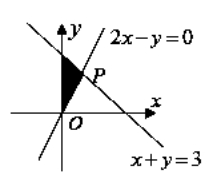
【名师点睛】若约束条件表示的可行域是封闭区域,则可以将顶点坐标代入目标函数,求出****值与最小值,从而得到相应范围.若约束条件表示的可行域不是封闭区域,则不能简单地运用代入顶点坐标的方法求最值.
5.D 【解析】采用排除法:A.令![]() 可排除此选项;B.令
可排除此选项;B.令![]() 可排除此选项;C.令
可排除此选项;C.令![]() 可排除此选项.故选D.
可排除此选项.故选D.
【方法点睛】对于判断不等式恒成立问题,一般采用举反例排除法.解答本题时能够对四个选项逐个利用赋值的方式进行排除,确认成立的不等式.
6.A 【解析】画圆:(x−1)2+(y−1)2=2,如图所示,则(x−1)2+(y−1)2≤2表示圆及其内部,设该区域为M.画出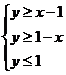 表示的可行域,如图中阴影部分所示,设该区域为N.可知N在M内,则p是q的必要不充分条件.故选A.
表示的可行域,如图中阴影部分所示,设该区域为N.可知N在M内,则p是q的必要不充分条件.故选A.
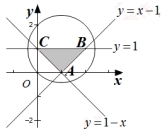
【名师点睛】本题考查充分性与必要性的判断问题,首先要分清条件和结论,然后看由条件推结论,由结论推条件是否成立.这类问题往往与函数、三角、不等式等数学知识相结合.本题的条件与结论可以转化为平面区域的关系,利用充分性、必要性和集合的包含关系可得出结论.
7.B 【解析】若乙盒中放入的是红球,则须保证抽到的两个均是红球;若乙盒中放入的是黑球,则须保证抽到的两个球是一红一黑,且红球放入甲盒;若丙盒中放入的是红球,则须保证抽到的两个球是一红一黑:且黑球放入甲盒;若丙盒中放入的是黑球,则须保证抽到的两个球都是黑球.由于抽到两个红球的次数与抽到两个黑球的次数应是相等的,故乙盒中红球与丙盒中黑球一样多,选B.
【名师点睛】本题创新味十足,是能力立意的好题.如果所求事件对应的基本事件有多种可能,那么一般我们通过逐一列举计数,再求概率,此题即是如此.列举的关键是要有序(有规律),从而确保不重不漏.另外注意对立事件概率公式的应用.
8.C 【解析】不等式组表示的可行域是以A(0,−3),B(0,2),C(3,−1)为顶点的三角形区域(包括![]() 内部及边界),
内部及边界),![]() 表示三角形区域内的点(x,y)到原点距离的平方,****值必在顶点处取到,经验证****值为
表示三角形区域内的点(x,y)到原点距离的平方,****值必在顶点处取到,经验证****值为![]() ,故选C.
,故选C.
【名师点睛】本题主要考查简单线性规划的应用,是一道基础题目.从历年高考题目来看,简单线性规划问题,是不等式中的基本问题,往往围绕目标函数最值的确定,涉及直线的斜率、两点间距离等,考查考生的绘图、用图能力,以及应用数学解决实际问题的能力.
9.B 【解析】可行域为一个三角形ABC及其内部,其中![]() ,直线
,直线![]() 过点B时
过点B时![]() 取最小值6,选B.
取最小值6,选B.
【名师点睛】对于线性规划问题,首先明确可行域对应的是封闭区域还是开放区域、分界线是实线还是虚线,其次确定目标函数的几何意义,是求直线的截距、两点间距离的平方、直线的斜率、还是点到直线的距离等等,最后结合图形确定目标函数的最值或值域.
10.![]() 【解析】由题意得:
【解析】由题意得:![]() ,即
,即![]() ,故解集为
,故解集为![]() .
.
【名师点睛】解****值不等式时,关键是去掉****值符号,然后再进一步求解,本题也可利用两边同时平方的方法.本题较为容易.
11.![]() 【解析】要使函数式有意义,必有
【解析】要使函数式有意义,必有![]() ,即
,即![]() ,解得
,解得![]() .故答案为
.故答案为![]() .
.
12.![]() 【解析】作出不等式组表示的平面区域,如图中阴影部分所示.由图知,当直线
【解析】作出不等式组表示的平面区域,如图中阴影部分所示.由图知,当直线![]() 经过点
经过点![]() 时,z取得****值.由
时,z取得****值.由![]() 得
得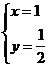 ,即
,即![]() ,则
,则![]() .
.
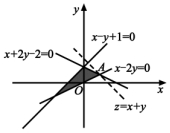
【技巧点拨】利用图解法解决线性规划问题的一般步骤:(1)作出可行域.将约束条件中的每一个不等式当作等式,作出相应的直线,并确定原不等式的区域,然后求出所有区域的交集;(2)作出目标函数的等值线(等值线是指目标函数过原点的直线);(3)求出最终结果.
13.![]() 【解析】画出不等式组表示的平面区域(图略),由图可知原点到直线
【解析】画出不等式组表示的平面区域(图略),由图可知原点到直线![]() 的距离的平方为
的距离的平方为![]() 的最小值,计算得最小值为
的最小值,计算得最小值为![]() ,原点到直线
,原点到直线![]() 与
与![]() 的交点
的交点![]() 的距离的平方为
的距离的平方为![]() 的****值,计算得****值为
的****值,计算得****值为![]() ,因此
,因此![]() 的取值范围为
的取值范围为![]()
【名师点睛】线性规划问题,首先明确可行域对应的是封闭区域还是开放区域、分界线是实线还是虚线(一般不涉及虚线),其次确定目标函数的几何意义,是求直线的截距、两点间距离的平方、直线的斜率、还是点到直线的距离等,最后结合图形确定目标函数的最值或值域.
14.![]() 【解析】设生产产品A、产品B分别为
【解析】设生产产品A、产品B分别为![]() 、
、![]() 件,利润之和为
件,利润之和为![]() 元,那么由题意得约束条件为
元,那么由题意得约束条件为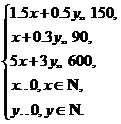 目标函数
目标函数![]() .约束条件等价于
.约束条件等价于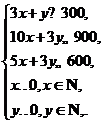 ①
①
作出二元一次不等式组①表示的平面区域,即可行域,如图中阴影部分所示.
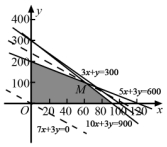
将![]() 变形,得
变形,得![]() ,作直线:
,作直线:![]() 并平移,当直线
并平移,当直线![]() 经过点
经过点![]() 时,
时,![]() 取得****值.解方程组
取得****值.解方程组![]() ,得
,得![]() 的坐标为
的坐标为![]() .
.
所以当![]() ,
,![]() 时,
时,![]() .
.
故生产产品A、产品B的利润之和的****值为![]() 元.
元.
【名师点睛】线性规划也是高考中常考的知识点,一般以客观题的形式出现,基本题型是给出约束条件求目标函数的最值,常见的结合方式有:纵截距、斜率、两点间的距离、点到直线的距离,解决此类问题常利用数形结合.本题运算量较大,失分的一个主要原因是运算失误.
15.1和3 【解析】由题意分析可知甲的卡片上的数字为1和3,乙的卡片上的数字为2和3,丙的卡片上的数字为1和2.
【名师点睛】逻辑推理即演绎推理,就是从一般性的前提出发,通过推导即“演绎”,得出具体陈述或个别结论的过程.