多维层次练46
[A级　基础巩固]
1．已知圆C：(x－6)2＋(y－8)2＝4，O为坐标原点，则以OC为直径的圆的方程为(　　)
A．(x－3)2＋(y＋4)2＝100
B．(x＋3)2＋(y－4)2＝100
C．(x－3)2＋(y－4)2＝25
D．(x＋3)2＋(y－4)2＝25
解析：圆C的圆心坐标为C(6，8)，
则OC的中点坐标为E(3，4)，
则所求圆的半径|OE|＝Ö3+Ö4＝5，
则以OC为直径的圆的方程为(x－3)2＋(y－4)2＝25.
故选C.
答案：C
2．(2020·青岛实验高中测试)方程x2＋y2＋ax＋2ay＋2a2＋a－1＝0表示圆，则a的取值范围是(　　)
A．a<－2   B．－<a<0
C．－2<a<0   D．－2<a<
解析：方程x2＋y2＋ax＋2ay＋2a2＋a－1＝0表示圆，
所以a2＋4a2－4(2a2＋a－1)>0，
所以3a2＋4a－4<0，
所以(a＋2)(3a－2)<0，所以－2<a<.
答案：D
3．平面内动点P到两点A、B距离之比为常数λ(λ＞0，且λ≠1)，则动点P的轨迹叫做阿波罗尼斯圆，若已知A(－2，0)，B(2，0)，λ＝，则此阿波罗尼斯圆的方程为(　　)
A．x2＋y2－12x＋4＝0   B．x2＋y2＋12x＋4＝0
C．x2＋y2－x＋4＝0   D．x2＋y2＋x＋4＝0
解析：由题意，设P(x，y)，则＝，
化简可得x2＋y2＋x＋4＝0，故选D.
答案：D
4．(2020·青岛实验高中测试)圆心为(2，－1)的圆，在直线x－y－1＝0上截得的弦长为2，那么，这个圆的方程为(　　)
A．(x－2)2＋(y＋1)2＝4 B．(x－2)2＋(y＋1)2＝2
C．(x＋2)2＋(y－1)2＝4 D．(x＋2)2＋(y－1)2＝2
解析：因为圆心到直线x－y－1＝0的距离d＝＝，弦长为2，
所以圆的半径r＝＝2，
则圆的方程为(x－2)2＋(y＋1)2＝4.
答案：A
5．(2020·聊城模拟)圆x2＋y2－6x－2y＋3＝0的圆心到直线x＋ay－1＝0的距离为1，则a＝(　　)
A．－   B．－ 
C.   D．2
解析：圆x2＋y2－6x－2y＋3＝0，即(x－3)2＋(y－1)2＝7，圆心(3，1)到直线x＋ay－1＝0的距离d＝＝1，所以a＝－.
答案：B
6．(2020·滨州市期末)已知圆的方程为x2＋y2－6x＝0，过点P(1，2)的该圆的所有弦中，最短弦的长为(　　)
A.   B．1 
C．2   D．4
解析：由x2＋y2－6x＝0，得(x－3)2＋y2＝9，
所以圆心坐标为(3，0)，半径为3.如图所示，

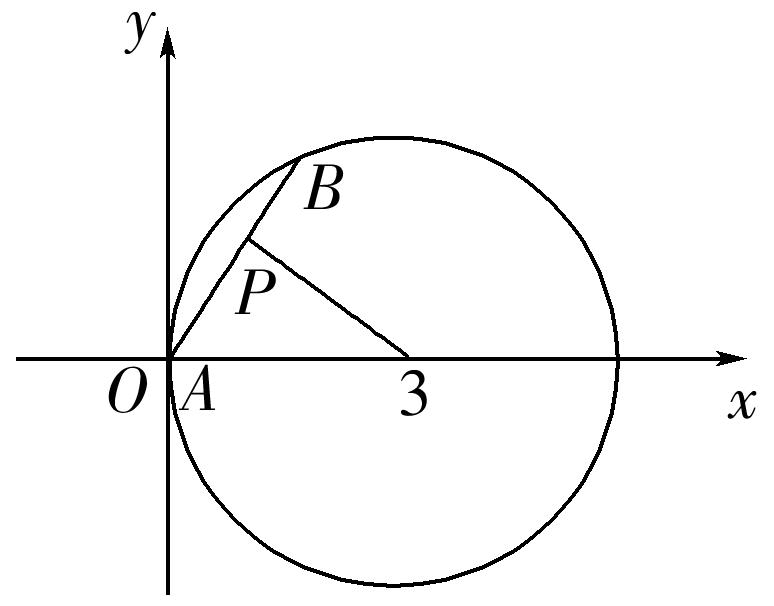
当过点P(1，2)的直线与连接P与圆心的直线垂直时，弦AB最短，
则最短弦长为2＝2.
答案：C
7．圆心在直线x＝2上的圆与y轴交于两点A(0，－4)，B(0，－2)，则该圆的标准方程为________________．
解析：由已知，得圆心的纵坐标为＝－3，
所以圆心为(2，－3)，
则半径r＝＝，
故所求圆的标准方程为(x－2)2＋(y＋3)2＝5.
答案：(x－2)2＋(y＋3)2＝5
8．已知点A(2，0)，B(0，2)，则以线段AB为直径的圆的方程是________．
解析：AB的中点为，即(1，1)．所以圆心为(1，1)．因为|AB|＝2，所以圆的半径为.所以所求圆的方程为(x－1)2＋(y－1)2＝2.
答案：(x－1)2＋(y－1)2＝2
9．(一题多解)在平面直角坐标系中，经过三点(0，0)，(1，1)，(2，0)的圆的方程为________．
解析：法一　根据题意画出图形，如图所示，结合图形知经过三点(0，0)，(1，1)，(2，0)的圆，其圆心为(1，0)，半径为1，则该圆的方程为(x－1)2＋y2＝1.

法二　设该圆的方程为x2＋y2＋Dx＋Ey＋F＝0，
则
解得D＝－2，E＝F＝0；
所以所求圆的方程为x2＋y2－2x＝0.
答案：(x－1)2＋y2＝1(或x2＋y2－2x＝0)
10．(2019·衡水中学调研)已知直角三角形ABC的斜边为AB，且A(－1，0)，B(3，0)．求：
(1)(一题多解)直角顶点C的轨迹方程；
(2)直角边BC的中点M的轨迹方程．
解：(1)法一　设C(x，y)，因为A，B，C三点不共线，
所以y≠0.
因为AC⊥BC，所以kAC·kBC＝－1，又kAC＝，kBC＝，
所以·＝－1，
化简得x2＋y2－2x－3＝0.
因此，直角顶点C的轨迹方程为x2＋y2－2x－3＝0(y≠0)．
法二　设AB的中点为D，由中点坐标公式得D(1，0)，由直角三角形的性质知|CD|＝|AB|＝2.由圆的定义知，动点C的轨迹是以D(1，0)为圆心，2为半径的圆(由于A，B，C三点不共线，所以应除去与x轴的交点)．
所以直角顶点C的轨迹方程为(x－1)2＋y2＝4(y≠0)．

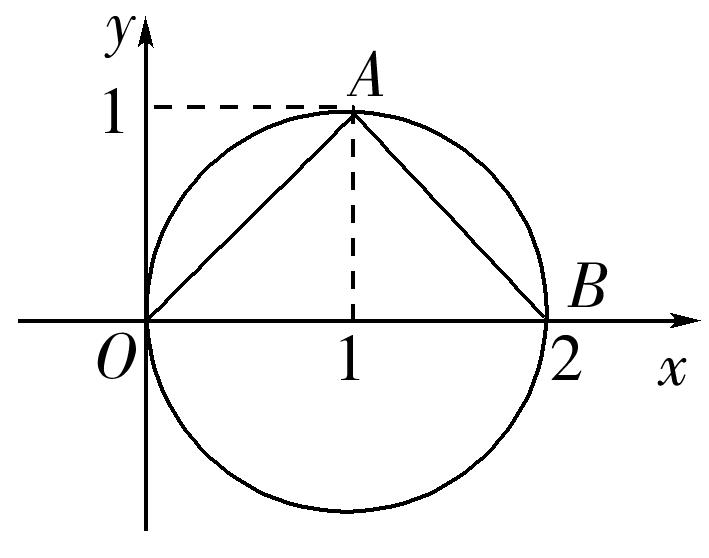
(2)设M(x，y)，C(x0，y0)，因为B(3，0)，M是线段BC的中点，由中点坐标公式得x＝，y＝，所以x0＝2x－3，y0＝2y.
由(1)知，点C的轨迹方程为(x－1)2＋y2＝4(y≠0)，
将x0＝2x－3，y0＝2y代入得(2x－4)2＋(2y)2＝4，
即(x－2)2＋y2＝1.
因此动点M的轨迹方程为(x－2)2＋y2＝1(y≠0)．
[B级　能力提升]
11．(2020·广州市期中)圆x2＋y2－2x＋4y－3＝0上到直线x＋y＋3＝0的距离为的点的个数为(　　)
A．1   B．2 
C．3   D．4
解析：圆x2＋y2－2x＋4y－3＝0即(x－1)2＋(y＋2)2＝8，
表示以C(1，－2)为圆心，以2为半径的圆．
圆心到直线x＋y＋3＝0的距离为d＝＝＝，
故圆x2＋y2－2x＋4y－3＝0上到直线x＋y＋3＝0的距离为的点共有4个．
答案：D
12．在平面直角坐标系xOy中，以点(1，0)为圆心且与直线mx－y－2m－1＝0(m∈R)相切的所有圆中，半径****的圆的标准方程为________．
解析：直线mx－y－2m－1＝0经过定点(2，－1)．
当圆与直线相切于点(2，－1)时，圆的半径****，此时半径r满足
r2＝(1－2)2＋(0＋1)2＝2.
此时圆的方程为(x－1)2＋y2＝2.
答案：(x－1)2＋y2＝2
13．(2020·聊城市期中)已知曲线方程为：x2＋y2－2x－4y＋m＝0.
(1)若此曲线是圆，求m的取值范围；
(2)若(1)中的圆与直线x＋2y－4＝0相交于M，N两点，且OM⊥ON(O是坐标原点)，求m的值．
解：(1)曲线方程为：x2＋y2－2x－4y＋m＝0.
整理得：(x－1)2＋(y－2)2＝5－m，
因为此曲线是圆，
所以5－m>0，解得m<5.
即m的取值范围是(－∞，5)．
(2)设直线x＋2y－4＝0与圆：x2＋y2－2x－4y＋m＝0的交点为M(x1，y1)，N(x2，y2)．
则
整理得：5y2－16y＋8＋m＝0，
Δ＝162－20(8＋m)>0，得m<.
则y1＋y2＝，y1y2＝，
由OM⊥ON(O为坐标原点)，则：x1x2＋y1y2＝0，
x1＝4－2y1，x2＝4－2y2，
则(4－2y1)(4－2y2)＋y1y2＝5y1y2－8(y1＋y2)＋16＝0.
解得m＝，符合，
故m的值为.
[C级　素养升华]
14．(2020·三环高中月考)过动点P作圆：(x－3)2＋(y－4)2＝1的切线PQ，其中Q为切点，若|PQ|＝|PO|(O为坐标原点)，则|PQ|的最小值是________．
解析：根据题意，设P的坐标为(m，n)，圆(x－3)2＋(y－4)2＝1的圆心为N，则N(3，4)，
PQ为圆(x－3)2＋(y－4)2＝1的切线，则有|PN|2＝|PQ|2＋|NQ|2＝|PQ|2＋1，
又由|PQ|＝|PO|，
则有|PN|2＝|PO|2＋1，

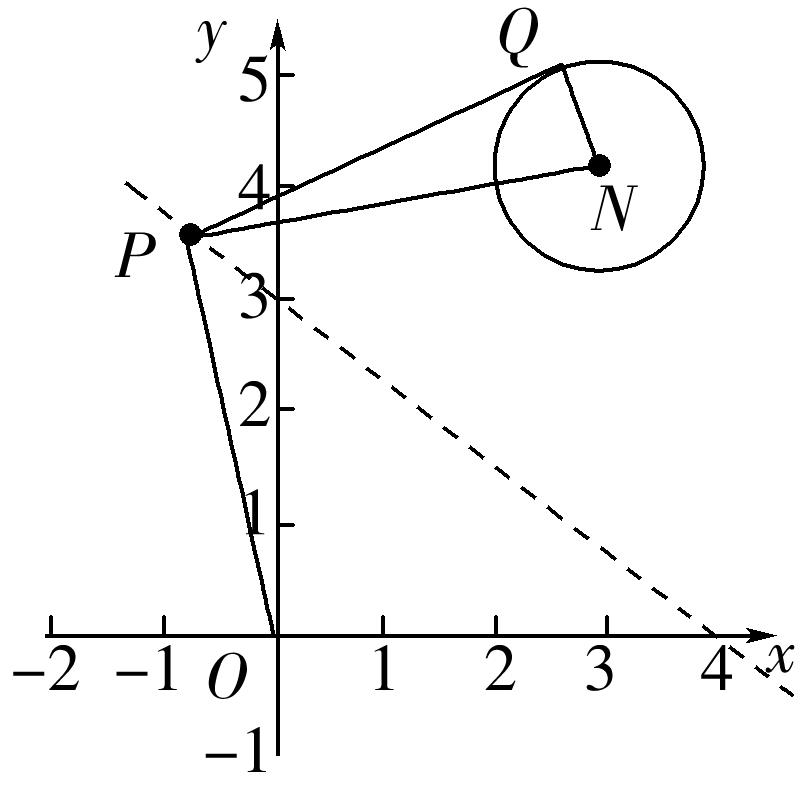
即(m－3)2＋(n－4)2＝m2＋n2＋1，
整理可得6m＋8n＝24，
即P在直线6x＋8y＝24上，
则|PQ|的最小值即点O到直线6x＋8y＝24的距离，
且d＝12/5，
即|PQ|的最小值是.
答案：