课题2：集合间的基本关系及运算

一、复习回顾：

1.提问：集合的两种表示方法？ 如何用适当的方法表示下列集合？

（1）10以内3的倍数；    

（2）1000以内3的倍数

2.用适当的符号填空： 0    N；     Q；  -1.5    R。

思考1：类比实数的大小关系，如5<7，2≤2，试想集合间是否有类似的“大小”关系呢？

二、新课教学

比较下面几个例子，试发现两个集合之间的关系：

（1），；

（2），；

（3），

1． 子集的定义：

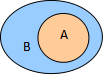对于两个集合A，B，如果集合A的任何一个元素都是集合B的元素，我们说这两个集合有包含关系，称集合A是集合B的子集（subset）。 记作：

  

读作：A包含于（is contained in）B，或B包含（contains）A

当集合A不包含于集合B时，记作

用Venn图表示两个集合间的“包含”关系：     如：（1）中 

2． 集合相等定义：

如果A是集合B的子集，且集合B是集合A的子集，则集合A与集合B中的元素是一样的，因此集合A与集合B相等，即若，则。

   如（3）中的两集合。

3． 真子集定义：

若集合，但存在元素，则称集合A是集合B的真子集（proper subset）。记作：

A  B（或B A） 

读作：A真包含于B（或B真包含A）

   如：（1）和（2）中A  B，C  D；

4． 空集定义：

不含有任何元素的集合称为空集（empty set），记作：。

用适当的符号填空：

     ； 0      ；      ；       

思考2：课本P7 的思考题

5． 几个重要的结论：

（1） 空集是任何集合的子集；

（2） 空集是任何非空集合的真子集；

（3） 任何一个集合是它本身的子集；

（4） 对于集合A，B，C，如果，且，那么。

说明：

1． 注意集合与元素是“属于”“不属于”的关系，集合与集合是“包含于”“不包含于”的关系；

2． 在分析有关集合问题时，要注意空集的地位。

课堂练习

1．填空：

（1）．  2   N；       N；          A;       

（2）．已知集合A＝{x|x－3x＋2＝0}，B＝{1,2}，C＝{x|x<8,x∈N}，则 

 A     B；    A     C；    {2}     C；      2     C

（3） 0   {0}；   0    Φ；  Φ   {x|x＋1＝0,x∈R} 

   {0}   {x|x<3且x>5}； {x|x>6}  {x|x<－2或x>5} ；  {x|x>－3}   {x>2}

2．写出集合的所有子集，并指出哪些是它的真子集。

  

3.课本P7练习1，2，3

4．已知A={1，2，3}，S={1，2，3，4，5}，则A   S；{x|x∈S且xA}=      。

5．若集合 B  A，求m的值。

6．已知集合且，

求实数m的取值范围。     

思考．考察下列集合，说出集合C与集合A，B之间的关系：

（1），；

6． 并集的定义：

一般地，由所有属于集合A或属于集合B的元素所组成的集合，叫做集合A与集合B的并集（union set）。记作：A∪B（读作：“A并B”），即

            

用Venn图表示：                                    

这样，在问题（1）（2）中，集合A，B的并集是C，即= C

说明：定义中要注意“所有”和“或”这两个条件。

讨论：A∪B与集合A、B有什么特殊的关系？

A∪A＝       ,  A∪Ф＝        ,  A∪B      B∪A

A∪B＝A            ,  A∪B＝B          .

巩固练习（口答）：  

①．A＝{3,5,6,8}，B＝{4,5,7,8}，则A∪B＝   ;

②．设A＝{锐角三角形}，B＝{钝角三角形}，则A∪B＝   ;  

 ③．A＝{x|x>3}，B＝{x|x<6}，则A∪B＝    。 

7． 交集的定义：

一般地，由属于集合A且属于集合B的所有元素组成的集合，叫作集合A、B的交集（intersection set），记作A∩B（读“A交B”）即：

A∩B＝{x|x∈A，且x∈B}

用Venn图表示：（阴影部分即为A与B的交集）

                      

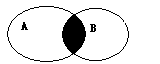
常见的五种交集的情况：

讨论：A∩B与A、B、B∩A的关系？

A∩A＝           A∩Ф＝              A∩B      B∩A

A∩B＝A                     A∩B＝B,           

巩固练习（口答）：

①．A＝{3,5,6,8}，B＝{4,5,7,8}，则A∩B＝   ;

②．A＝{等腰三角形}，B＝{直角三角形}，则A∩B＝     ;  

 ③．A＝{x|x>3}，B＝{x|x<6}，则A∩B＝    。 

1．（课本例5）设集合，求A∪B．

变式：A＝{x|-5≤x≤8}

2.课本P11练习1，2，3

3．已知集合

 是否存在实数m，同时满足？

8． 全集的定义：

一般地，如果一个集合含有我们所研究问题中涉及的所有元素，那么就称这个集合为全集（universe set）,记作U，是相对于所研究问题而言的一个相对概念。

9． 补集的定义：

对于一个集合A，由全集U中不属于集合A的所有元素组成的集合，叫作集合A相对于全集U的补集（complementary set），记作：，

读作：“A在U中的补集”，即

用Venn图表示：（阴影部分即为A在全集U中的补集）

讨论：集合A与之间有什么关系？→借助Venn图分析

     

巩固练习（口答）：

①．U={2,3,4}，A={4,3}，B=φ，则=     ，=     ；

②．设U＝{x|x<8，且x∈N}，A＝{x|(x-2)(x-4)(x-5)＝0}，则＝      ；

1．设集，求，．

2.课本P11练习4

3．设全集，求，

    ，。

    

4．设全集U为R，，若

 ，求。  

课下作业：

1．设求， 

2、已知，，若，求  

3. 设全集，求实数a的值。

4.设全集若,求、.