函数的概念
区间及写法:
设a、b是两个实数,且a<b,则:
(1) 满足不等式![]() 的实数x的集合叫做闭区间,表示为
的实数x的集合叫做闭区间,表示为
(2) 满足不等式![]() 的实数x的集合叫做开区间,表示为
的实数x的集合叫做开区间,表示为
(3) 满足不等式![]() 的实数x的集合叫做半开半闭区间,表示为
的实数x的集合叫做半开半闭区间,表示为
这里的实数a和b都叫做相应区间的端点。(数轴表示见课本P17表格)
符号“∞”读“无穷大”;“-∞”读“负无穷大”;“+∞”读“正无穷大”。我们把满足![]() 的实数x的集合分别表示为
的实数x的集合分别表示为
巩固练习:
1.用区间表示
R、 {x|x≥1} 、{x|x>5} 、
{x|x≤-1} 、{x|x<0}
2.用区间表示下列集合:
![]()
例题讲解:
例1、 下列四个图像中,是函数图像的是
下列四个图像中,是函数图像的是
A、① B、①③④ C、①②③ D、③④
例2.已知函数![]() ,求f(0)、f(1)、f(2)、f(-1)的值。
,求f(0)、f(1)、f(2)、f(-1)的值。![]() 、
、![]() 、
、![]() 。
。
变式:求函数![]() 的值域
的值域
例3.已知函数![]() ,
,
(1) 求![]() 的值;
的值;
(2) 当a>0时,求![]() 的值。
的值。
例4. 已知函数f(x)=3x![]() +5x-2,求f(3)、f(-
+5x-2,求f(3)、f(-![]() )、f(a)、f(a+1)的值;
)、f(a)、f(a+1)的值;
例5.函数![]() ,则
,则![]() = ,
= ,![]() 。
。
例7.若![]() ,则
,则![]() ,
,![]()
例6.设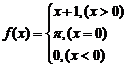 ,求
,求![]() ,
,![]() 的值。
的值。
(二)函数相同的判别方法:
函数是否相同,看定义域和对应法则。
例7.(课本P18例2)下列函数中哪个与函数y=x相等?
(1)![]() ; (2)
; (2)![]() ;
;
(3)![]() ; (4)
; (4) ![]() 。
。
什么叫函数?其三要素是什么?函数y=![]() 与y=3x是不是同一个函数?为什么?
与y=3x是不是同一个函数?为什么?
例8. 下列各组中的两个函数是否为相同的函数?
①![]()
![]()
![]()
②![]()
![]()
③![]()
![]()
例9、下列各组函数是同一函数的是 ( )
①![]() 与
与![]() ;②
;②![]() 与
与![]() ;③
;③![]() 与
与![]() ;④
;④![]() 与
与![]() 。
。
A、①② B、①③ C、③④ D、①④
函数定义域的求法:
函数的定义域通常由问题的实际背景确定,如果只给出解析式y=f(x),而没有指明它的定义域,那么函数的定义域就是指能使这个式子有意义的实数的集合。
例10:求下列函数的定义域(用区间表示)
⑴ f(x)=![]() ; ⑵ f(x)=
; ⑵ f(x)=![]() ; ⑶ f(x)=
; ⑶ f(x)=![]() -
-![]() ;
;
例11.求下列函数的定义域:
(1)![]() ;(2)
;(2)![]() (3)
(3)![]() ;
;
(4)![]() . (5)
. (5)![]()
例12.函数![]() 的定义域是
的定义域是