数列与新背景、新定义的综合问题

　(2014·东莞一模)如图,有一个形如六边形的点阵,它的中心是1个点(算第1层),第2层每边有2个点,第3层每边有3个点,依次类推.

(1) 第n(n≥2)层的点数为　　　　;

(2) 如果一个六边形点阵共有169个点,那么它一共有　　　　层.

(例1)

[思维引导](1) 可将第1,2,3,4,5层的点数一一列出,组成数列,然后判断数列的特点,猜出结论;(2) 根据(1)的结果求解.

[答案](1) 6(n-1)　(2) 8

[解析](1) 第1层的点数为1,第2层的点数为6,第3层的点数为12,第4层的点数为18,第5层的点数为24,它们组成数列:1,6,12,18,24,分别记为a₁,a₂,a₃,a₄,a₅.

因为a₃-a₂=6,a₄-a₃=6,a₅-a₄=6,猜想a_n-a_n-1=6(n≥2),

所以当n≥2时,由等差数列的通项公式可知a_n=a₂+(n-2)d=6+(n-2)×6=6(n-1),即a_n=6(n-1)(n≥2).

(2) 由(1)得+1=169,解得n=8.

[精要点评](1) 对于数列与新背景、新定义的综合问题,此类问题出题背景广、新颖,解题的关键是读懂题意,有效地将信息转化,能较好地考查学生分析、解决问题的能力和知识的迁移能力.一般以客观题或解答题的形式出现,属于低、中档题.

(2) 解决数列与新背景、新定义的综合问题,可通过对新数表、图象、新定义的分析、探究,将问题转化为等差(比)数列的问题.

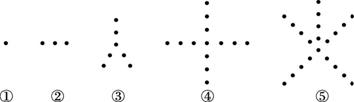
　根据图中的5个图形及相应点的个数的变化规律,试猜测第n个图中有　　　　个点.

(变式)

[答案]n²-n+1

[解析]序号n决定了每个图的分支数,而第n个分支有(n-1)个点,中心再加1点,故有n(n-1)+1=n²-n+1个点.

数列与函数、不等式等综合问题

　若数列{a_n}的前n项和记为S_n,a₁=t,点(S_n,a_n+1)在直线y=2x+1上,n∈N^*.

(1) 当实数t为何值时,数列{a_n}是等比数列?

(2) 在(1) 的结论下,设b_n=log₃a_n+1,T_n是数列的前n项和,求T_{2 015}的值.

[思维引导]解答本题需要掌握以下几个关键的知识点:(1) 利用前n项和与通项的关系;(2) 用裂项相消法求数列的前n项和.

[解答](1) 由题意得a_n+1=2S_n+1,a_n=2S_n-1+1(n≥2),

两式相减,得a_n+1-a_n=2a_n,即a_n+1=3a_n(n≥2),

所以当n≥2时,{a_n}是等比数列.

要使{a_n}是等比数列,则需==3,

从而得出t=1.

(2) 由(1)知a_n=3^n-1,b_n=log₃a_n+1=n,

==-,

T_{2 015}=+…+=++…+=.

[精要点评]本题以函数为背景,考查数列前n项和与通项的关系、等比数列、对数知识、裂项求前n项和等问题,内容较综合,但难度一般.

　(2014·扬州模拟)设函数f(x)=(x>0),数列{a_n}满足a₁=1,a_n=f(n∈N^*,n≥2),求数列{a_n}的通项公式.

[解答]因为a_n=f==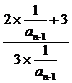a_n-1+(n∈N^*,且n≥2),

所以a_n-a_n-1=(n≥2).

因为a₁=1,所以数列{a_n}是以1为首项、为公差的等差数列,

所以a_n=.