4. 等差数列当首项a₁>0且公差d<0，前n项和存在****值。利用不等式组：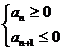

确定n值，即可求得S_n的****值。等差数列当首项a₁<0且公差d>0时，前n项和存在最小值。 类似地确定n值，即可求得s_n的最小值；也可视s_n为关于n的二次函数，通过配方求最值；还可以利用二次函数的图象来求。

 设等差数列满足3 a₈=5a₁₃，且a₁>0，则的前__________项和****

解析：思路一：由3 a₈=5a₁₃得：d=a₁,若前n项和****，则，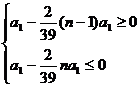

又a₁>0得：，∴n=20,即的前20项和****。这一做法最通行。

思路二：S_n=na₁+n(n-1)d=na₁- n(n-1)a₁=-a₁(n²-40n),当且仅当n=20时S_n****。这一做法突显了数列的函数特征。思路三：由3 a₈=5a₁₃得15a₈=25a₁₃,即S₁₅=S₂₅,又∵a₁>0，

∴S_n的图象是开口向下的抛物线上的点列，对称轴恰为n=20，故n=20时S_n****。这一做法中几乎没有运算，但设计太过“精妙”，非对等差数列的性质融会贯通而不能为，仅供欣赏。

 数列是等差数列，是其前n项和，且S₅＜S₆，S₆=S₇>S₈，则下列结论错误的是：A.d ＜0   B.a₇=0   C.S₉>S₅    D. S₆ ,S₇均为的****值   （    ）

 在等差数列则在前n项和S_n中****的负数为

         A．S₁₆         B．S₁₇         C．S₁₈         D．S₁₉            （     ）  

5.注意：等比数列求和公式是一个分段函数        na₁            (q=1)

                                        Sn=   

则涉及到等比数列求和时若公比不是具体数值须分类讨论解题。

已知等比数列的公比为q，前n项和为S_n，且S₃ ，S₉ ，S₆ 成等差数列，求q³的值。

解析：不可直接用等比数列的求和公式，需讨论：若q=1，S₃=3a₁ ，S₉=9a₁，S₆=6a₁,则有：

18a₁=3a₁+6a₁, 则a₁=0, 与是等比数列矛盾，∴q≠1，于是有：

，化简得：，∴。

本题还可以用：第一个三项和、第二个三项和、第三个三项和成等比数列解决，留读者自己完成。

已知a_n=1+r+r²+r³+…r^n-1，则数列的前n项和=______________

6.解等差（比）数列有关通项、求和问题时别忘了“基本元”，即把问题转化为首项a₁，公差d（或公比q）的方程（组）或不等式（组）去处理。已知等差或等比数列中的任两项也可用 a_m-a_n=(m-n)d，或=q^m-n。

 等差数列的前n项和S_n，若S₃=9，S₁₃=26求S₂₃的值。

解析：用求和公式解方程组，求出a₁,d,再代入求和公式中求S₂₃，这是通法。也可简化为：

S₃=3a₂=9a₂=3，S₁₃=13a₇=26a₇=2, ∴a₁₂= 1(a₂、a₇、a₁₂成等差数列)，S₂₃=23a₁₂=23。

已知等差数列{a_n}中，a₃与a₅的等差中项等于2，又a₄与a₆的等比中项等于6，则a₁₀等于  (A) 54     (B) 50     (C) 26     (D) 16

解析：a₃与a₅的等差中项等于2，即a₄=2；a₄与a₆的等比中项等于6，即a₆=18；于是2d=16,

a₁₀= a₆+4d=50,选B。