![]() 1 知识积累
1 知识积累
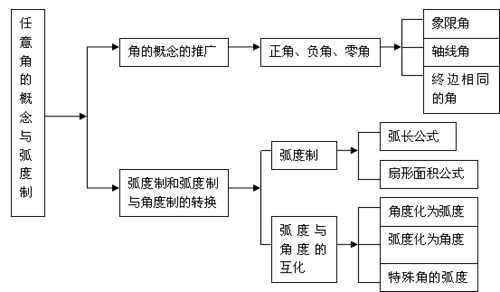
1、知识框架图:
2、知识了解
一、任意角
1.任意角的概念
角可以看成平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形。一条射线由原来的位置![]() ,绕着它的端点
,绕着它的端点![]() 按逆时针方向旋转到终止位置
按逆时针方向旋转到终止位置![]() ,就形成角
,就形成角![]() 。旋转开始时的射线
。旋转开始时的射线![]() 叫做角的始边,
叫做角的始边,![]() 叫终边,射线的端点
叫终边,射线的端点![]() 叫做叫
叫做叫![]() 的顶点。
的顶点。
在图中,射线![]() 绕端点
绕端点![]() 旋转到
旋转到![]() 位置所成的角,记作
位置所成的角,记作![]() ,其中
,其中![]() 叫做
叫做![]() 的始边,
的始边,![]() 叫做
叫做![]() 的终边。
的终边。
2.角的概念的推广
①按旋转方向不同分为正角、负角、零角. ②按终边位置不同分为象限角和轴线角.
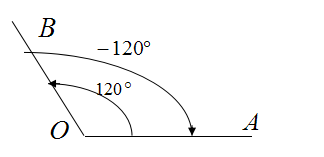
正角:按逆时针方向旋转所形成的角叫正角.
负角:按顺时针方向旋转所形成的角叫负角.
零角:如果一条射线没有做任何旋转,我们称它形成了一个零角。
象限角:角的顶点与原点重合,角的始边与![]() 轴的非负半轴重合。那么,角的终边(除端点外)在第几象限,我们就说这个角是第几象限角
轴的非负半轴重合。那么,角的终边(除端点外)在第几象限,我们就说这个角是第几象限角
轴线角:如果角的终边在坐标轴上,就认为这个角不属于任何一个象限,称为非象限角,即轴线角。
3.终边相同的角
终边相同的角指:所有与角α终边相同的角,连同角α在内,构成的角的集合是S={β|β=k·360°+α,k![]() }
}
注意:相等的角终边一定相同,终边相同的角不一定相等,终边相同的角有无数个,它们相差![]() 的整数倍。
的整数倍。
各象限角的集合与轴线角的集合
(1)象限角的集合
第一象限角集合为![]()
第二象限角的集合为![]()
第三象限角的集合为![]()
第四象限角的集合为![]()
(2)轴线角的集合
终边落在![]() 轴的非负半轴上,角的集合为
轴的非负半轴上,角的集合为![]()
终边落在![]() 轴的非正半轴上,角的集合为
轴的非正半轴上,角的集合为![]()
终边落在![]() 轴上,角的集合为
轴上,角的集合为![]()
终边落在![]() 轴的非负半轴上,角的集合为
轴的非负半轴上,角的集合为![]()
终边落在![]() 轴的非正半轴上,角的集合为
轴的非正半轴上,角的集合为![]()
终边落在![]() 轴上,角的集合为
轴上,角的集合为![]()
终边落在坐标轴上,角的集合为![]()
注意:终边落在同一条直线上的角相差![]() 的整数倍,终边落在同一条射线上的角相差
的整数倍,终边落在同一条射线上的角相差![]() 的整数倍。
的整数倍。
二.弧度制
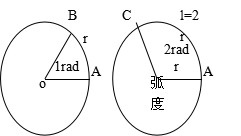 (1)定义:长度等于半径长的圆弧所对的圆心角叫做1弧度角,记作1
(1)定义:长度等于半径长的圆弧所对的圆心角叫做1弧度角,记作1![]() ,或1弧度,或1(单位可以省略不写)。角有正负零角之分,它的弧度数也应该有正负零之分,
,或1弧度,或1(单位可以省略不写)。角有正负零角之分,它的弧度数也应该有正负零之分,
正角的弧度数是一个正数,
负角的弧度数是一个负数,
零角的弧度数是0,
角的正负主要由角的旋转方向来决定。
(2)用“弧度”做单位来度量角的制度叫做弧度制,角![]() 的弧度数的****值是:
的弧度数的****值是:![]() ,其中,
,其中,![]() 是圆心角所对的弧长,
是圆心角所对的弧长,![]() 是半径。角度制与弧度制的换算主要抓住
是半径。角度制与弧度制的换算主要抓住![]() 。
。
(3)弧度与角度互换公式:1rad=![]() ≈57.30
≈57.30![]() °=57°18ˊ、1°=
°=57°18ˊ、1°=![]() ≈0.01745(rad)。
≈0.01745(rad)。
(4)扇形弧长公式:![]() (
(![]() 是圆心角的弧度数),扇形面积公式:
是圆心角的弧度数),扇形面积公式:![]() 。.
。.
(5)需记住的几个特殊角的弧度数
|
度 |
|
|
|
|
|
|
|
|
|
|
|
弧度 |
|
|
|
|
|
|
|
|
|
|
|
度 |
|
|
|
|
|
|
|
|
|
|
|
弧度 |
|
|
|
|
|
|
|
|
|
三.角的终边对称问题
①若角![]() 与角
与角![]() 的终边关于
的终边关于![]() 轴对称,则
轴对称,则![]() ;
;
②若角![]() 与角
与角![]() 的终边关于
的终边关于![]() 轴对称,则
轴对称,则![]() ;
;
③若角![]() 与角
与角![]() 的终边关于原点对称,则
的终边关于原点对称,则![]() ;
;
④若角![]() 与角
与角![]() 的相互垂直,则
的相互垂直,则![]() 。
。