1.知识积累

一、对称点的坐标

关于轴的对称坐标；关于轴的对称坐标

关于原点的对称坐标；关于的对称坐标

关于的对称坐标

二、诱导公式

诱导公式（一）

结构特征：①终边相同的角的同一三角函数值相等

②把求任意角的三角函数值问题转化为求～角的三角函数值问题。

诱导公式（二）

结构特征：①函数名不变，符号看象限（把看作锐角时）

②把求（）的三角函数值转化为求的三角函数值。

诱导公式（三）

结构特征：①函数名不变，符号看象限（把看作锐角）

②把求（）的三角函数值转化为求的三角函数值

诱导公式（四）

诱导公式（五）  

诱导公式（六）    

方法点拨：把看作锐角

前四组诱导公式可以概括为：函数名不变，符号看象限

的三角函数值，等于它的同名三角函数值，前面加上一个把看成锐角时原函数值的符号。

公式（五）和公式（六）总结为一句话：函数名改变，符号看象限

三、奇变偶不变，符号看象限

将三角函数的角度全部化成或是，符号名该不该变就看是奇数还是偶数，是奇数就改变函数名，偶数就不变。符号看函数所在象限。

四、利用诱导公式可以把任意角的三角函数转化为锐角三角函数

利用诱导公式把任意角的三角函数转化为锐角三角函数的基本步骤是：

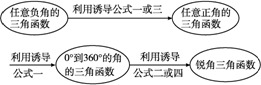
可以看出，这些步骤体现了把未知问题化归为已知问题的数学思想．可以简单记为“负化正，大化小，化成锐角才罢了”．

六、诱导公式综合

	－
sin	－sin	sin	－sin	－sin	sin	cos
cos	cos	－cos	－cos	cos	cos	sin
tan	－tan	－tan	tan	－tan	tan	cot

七、其他公式

（1）sin(kπ+α)=(－1)ksinα；cos(kπ+α)=(－1)kcosα(k∈Z)；

（2）；。

<, IMG alt=学科网(www.zxxk.com)--教育资源门户，提供试卷、教案、课件、论文、素材及各类教学资源下载，还有大量而丰富的教学相关资讯！ src="/UploadFiles/20151218163702190.gif" width=32 height=32 v:shapes="Picture_x0020_3">2.典型例题

【例1】 求下列三角函数式的值．

(1)sin 1320°；(2)cos(－π)；(3)tan(－945°)．

解：(1)法一：sin 1320°＝sin(3×360°＋240°)＝sin 240°＝sin(180°＋60°)＝－sin 60°＝－.

法二：sin 1320°＝sin(4×360°－120°)＝sin(－120°)＝－sin(180°－60°)＝－sin 60°＝－.

(2)法一：cos(－)＝cos＝cos(4π＋)＝cos(π＋)＝－cos＝－.

变式训练11：计算下列各式的值：

(1)sin 600°＋tan 240°；(2)sin 15°cos 75°＋cos 15°sin 75°.

解：(1)sin 600°＋tan 240°＝sin(360°＋240°)＋tan(180°＋60°)＝sin 240°＋tan 60°＝－sin 60°＋tan 60°＝.

(2)sin 15°cos 75°＋cos 15°sin 75°＝sin² 15°＋cos² 15°＝1.

【例2】 已知cos(π＋α)＝－，求sin(2π－α)的值．

解：∵cos(π＋α)＝－cos α＝－，∴cos α＝，∴α是第一或第四象限角．

①若α是第一象限角，则sin(2π－α)＝－sin α＝－＝－.

②若α是第四象限角，则sin(2π－α)＝－sin α＝＝.

变式训练21：已知sin(－α)＝，则cos(＋α)＝________.

解析：∵(－α)＋(＋α)＝，∴cos(＋α)＝cos[－(－α)]＝sin(－α)＝.

【例3】 求证：＝－tan α.

证明：原式左边＝＝＝－＝－tan α＝右边．

∴原式得证．

变式训练31：已知△ABC的三个内角分别为A，B，C，证明：

(1)cos A＋cos(B＋C)＝0；(2)sin＝cos.

证明：(1)∵A＋B＋C＝π，∴B＋C＝π－A，∴cos A＋cos(B＋C)＝cos A＋cos(π－A)＝cos A－cos A＝0；

(2)∵＝＝－，∴sin＝sin(－)＝cos.

【例4】 化简cos(π＋x)＋cos(π－x)(n∈Z)．

解：原式＝cos(nπ＋＋x)＋cos(nπ－－x)．

(1)当n为奇数，即n＝2k＋1(k∈Z)时，

原式＝cos＋cos＝－cos(＋x)－cos(－－x)＝－2cos(＋x)；

(2)当n为偶数，即n＝2k(k∈Z)时，

原式＝cos(2kπ＋＋x)＋cos(2kπ－－x)＝cos(＋x)＋cos(－－x)＝2cos(＋x)．

故原式＝

变式训练41：已知：sin(π＋θ)＝－，求值：＋.

解：原式＝＋＝＋＝，

∵sin(π＋θ)＝－，∴sin(π＋θ)＝－sin θ＝－，∴sin θ＝，∴原式＝＝18