1．已知命题p：所有有理数都是实数；命题q：正数的对数都是负数，则下列命题中为真命题的是(　　)

A．(綈p)∨q B．p∧q

C．(綈p)∧(綈q)   D．(綈p)∨(綈q)

【答案】　D

【解析】　不难判断命题p为真命题，命题q为假命题，从而上述叙述中只有(綈p)∨(綈q)为真命题．

2．已知命题p，q，“綈p为真”是“p∧q为假”的(　　)

A．充分不必要条件

B．必要不充分条件

C．充要条件

D．既不充分也不必要条件

【答案】　A

【解析】　由“綈p为真”可得p为假，故p∧q为假；反之不成立．

3．已知命题p：“x>2是x2>4的充要条件”，命题q：“若c2(a)>c2(b)，则a>b”，那么(　　)

A．“p或q”为真 B．“p且q”为真

C．p真q假 D．p，q均为假

【答案】　A

【解析】　由已知得命题p是假命题，命题q是真命题，因此选A.

4．下列命题中的假命题是(　　)

A．∀x∈R,2x－1>0 B．∀x∈N*，(x－1)2>0

C．∃x0∈R，lgx0<1 D．∃x0∈R，tan4(π)＝5

【答案】　B

5．已知命题p：若a>1，则ax>logax恒成立；命题q：在等差数列{an}中，m＋n＝p＋q是an＋am＝ap＋aq的充分不必要条件(m，n，p，q∈N*)．则下面选项中真命题是(　　)

A．(綈p)∧(綈q)   B．(綈p)∨(綈q)

C．p∨(綈q)   D．p∧q

【答案】　B

【解析】　当a＝1.1，x＝2时，

ax＝1.12＝1.21，logax＝log1.12>log1.11.21＝2，

6．命题p：∀x∈R，sinx<1；命题q：∃x∈R，cosx≤－1，则下列结论是真命题的是(　　)

A．p∧q B．(綈p)∧q

C．p∨(綈q)   D．(綈p)∧(綈q)

答案　B

解析　p是假命题，q是真命题，所以B正确．

7．已知命题p：所有指数函数都是单调函数，则綈p为(　　)

A．所有的指数函数都不是单调函数

B．所有的单调函数都不是指数函数

C．存在一个指数函数，它不是单调函数

D．存在一个单调函数，它不是指数函数

答案　C

解析　命题p：所有指数函数都是单调函数，则綈p：存在一个指数函数，它不是单调函数.

8．已知命题p：∃x0∈R，ex0－mx0＝0，q：∀x∈R，x2＋mx＋1≥0，若p∨(綈q)为假命题，则实数m的取值范围是(　　)

A．(－∞，0)∪(2，＋∞)   B．

C．R D．∅

答案　B

解析　若p∨(綈q)为假命题，则p假q真．命题p为假命题时，有0≤m<e；命题q为真命题时，有Δ＝m2－4≤0，即－2≤m≤2.所以当p∨(綈q)为假命题时，m的取值范围是0≤m≤2.

9．命题“∃x∈R，使得x2＋2x＋5＝0”的否定是________．

答案　∀x∈R，x2＋2x＋5≠0

解析　否定为全称命题：“∀x∈R，x2＋2x＋5≠0”．

10．若命题“∃x0∈R，x0(2)＋(a－1)x0＋1<0”是真命题，则实数a的取值范围是________．

答案　(－∞，－1)∪(3，＋∞)

解析　因为命题“∃x0∈R，x0(2)＋(a－1)x0＋1<0”等价于x0(2)＋(a－1)x0＋1＝0有两个不等的实根，所以Δ＝(a－1)2－4>0，即a2－2a－3>0，解得a<－1或a>3.

11．已知命题p：x2＋2x－3>0；命题q：3－x(1)>1，若“綈q∧p”为真，则x的取值范围是________．

答案　(－∞，－3)∪(1,2]∪

解析　若綈p是假命题，则p是真命题，

即关于x的方程4x－2·2x＋m＝0有实数解，

由于m＝－(4x－2·2x)＝－(2x－1)2＋1≤1，

∴m≤1.

17．设p：方程x2＋2mx＋1＝0有两个不相等的正根；q：方程x2＋2(m－2)x－3m＋10＝0无实根．则使p∨q为真，p∧q为假的实数m的取值范围是________．

答案　(－∞，－2]∪[－1,3)

18．已知f(x)＝m(x－2m)(x＋m＋3)，g(x)＝2x－2.若同时满足条件：

①∀x∈R，f(x)<0或g(x)<0；

②∃x∈(－∞，－4)，f(x)g(x)<0，

则m的取值范围是________．

答案　(－4，－2)

解析　当x≥1时，g(x)≥0，∴要满足条件①，则f(x)<0在x≥1时恒成立，f(x)＝m(x－2m)(x＋m＋3)为二次函数，抛物线必须开口向下，即m<0.f(x)＝0的两根x1＝2m，x2＝－m－3，且x1－x2＝3m＋3.

(ⅰ)当x1>x2，即－1<m<0时，必须大根x1＝2m<1，即m<2(1).∴此时－1<m<0；

(ⅱ)当x1<x2，即m<－1时，大根x2＝－m－3<1，即m>－4.∴此时－4<m<－1；

(ⅲ)当x1＝x2，即m＝－1时，x1＝x2＝－2<1也满足条件．

∴满足条件①的m的取值范围为－4<m<0.

满足条件②∃x∈(－∞，－4)，f(x)g(x)<0，必须满足二次函数的小根小于－4.

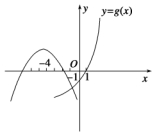
(ⅰ)当m>－1时，小根x2＝－m－3<－4且m<0，无解．

(ⅱ)当m<－1时，小根x1＝2m<－4且m<0，解得m<－2.

(ⅲ)当m＝－1时，f(x)＝－(x＋2)2≤0恒成立，

∴不满足②.

∴满足①②的m的取值范围是－4<m<－2.