充分条件与必要条件
【学习目标】
1.理解充分条件、必要条件、充要条件的定义;
2.会求某些简单问题成立的充分条件、必要条件、充要条件;
3.会应用充分不必要条件、必要不充分条件、充要条件、既不充分也不必要条件表达命题之间的关系.
4.能够利用命题之间的关系判定充要关系或进行充要性的证明.
【要点梳理】
要点一、充分条件与必要条件 充要条件的概念
符号![]() 与
与![]() 的含义
的含义
“若![]() ,则
,则![]() ”为真命题,记作:
”为真命题,记作:![]() ;
;
“若![]() ,则
,则![]() ”为假命题,记作:
”为假命题,记作:![]() .
.
充分条件、必要条件与充要条件
①若![]() ,称
,称![]() 是
是![]() 的充分条件,
的充分条件,![]() 是
是![]() 的必要条件.
的必要条件.
②如果既有![]() ,又有
,又有![]() ,就记作
,就记作![]() ,这时
,这时![]() 是
是![]() 的充分必要条件,称
的充分必要条件,称![]() 是
是![]() 的充要条件.
的充要条件.
要点诠释:对![]() 的理解:指当
的理解:指当![]() 成立时,
成立时,![]() 一定成立,即由
一定成立,即由![]() 通过推理可以得到
通过推理可以得到![]() .
.
①“若![]() ,则
,则![]() ”为真命题;
”为真命题;
②![]() 是
是![]() 的充分条件;
的充分条件;
③![]() 是
是![]() 的必要条件
的必要条件
以上三种形式均为“![]() ”这一逻辑关系的表达.
”这一逻辑关系的表达.
要点二、充分条件、必要条件与充要条件的判断
从逻辑推理关系看
命题“若![]() ,则
,则![]() ”,其条件p与结论q之间的逻辑关系
”,其条件p与结论q之间的逻辑关系
①若![]() ,但
,但![]() ,则
,则![]() 是
是![]() 的充分不必要条件,
的充分不必要条件,![]() 是
是![]() 的必要不充分条件;
的必要不充分条件;
②若![]() ,但
,但![]() ,则
,则![]() 是
是![]() 的必要不充分条件,
的必要不充分条件,![]() 是
是![]() 的充分不必要条件;
的充分不必要条件;
③若![]() ,且
,且![]() ,即
,即![]() ,则
,则![]() 、
、![]() 互为充要条件;
互为充要条件;
④若![]() ,且
,且![]() ,则
,则![]() 是
是![]() 的既不充分也不必要条件.
的既不充分也不必要条件.
从集合与集合间的关系看
若p:x∈A,q:x∈B,
①若A![]() B,则
B,则![]() 是
是![]() 的充分条件,
的充分条件,![]() 是
是![]() 的必要条件;
的必要条件;
②若A是B的 真子集,则![]() 是
是![]() 的充分不必要条件;
的充分不必要条件;
③若A=B,则![]() 、
、![]() 互为充要条件;
互为充要条件;
④若A不是B的子集且B不是A的子集,则![]() 是
是![]() 的既不充分也不必要条件.
的既不充分也不必要条件.
要点诠释:充要条件的判断通常有四种结论:充分不必要条件、必要不充分条件、充要条件、既不充分也不必要条件.判断方法通常按以下步骤进行:
①确定哪是条件,哪是结论;
②尝试用条件推结论,
③再尝试用结论推条件,
④最后判断条件是结论的什么条件.
要点三、充要条件的证明
要证明命题的条件是结论的充要条件,既要证明条件的充分性(即证原命题成立),又要证明条件的必要性(即证原命题的逆命题成立)
要点诠释:对于命题“若![]() ,则
,则![]() ”
”
①如果![]() 是
是![]() 的充分条件,则原命题“若
的充分条件,则原命题“若![]() ,则
,则![]() ”与其逆否命题“若
”与其逆否命题“若![]() ,则
,则![]() ”为真命题;
”为真命题;
②如果![]() 是
是![]() 的必要条件,则其逆命题“若
的必要条件,则其逆命题“若![]() ,则
,则![]() ”与其否命题“若
”与其否命题“若![]() ,则
,则![]() ”为真命题;
”为真命题;
③如果![]() 是
是![]() 的充要条件,则四种命题均为真命题.
的充要条件,则四种命题均为真命题.
【典型例题】
类型一:充分条件、必要条件、充要条件的判定
例1. “x<-1”是“x2-1>0”的________条件.
【解析】![]() ,故
,故![]() ,但
,但![]() ,
,
∴“x<-1”是“x2-1>0”的充分而不必要条件.
【点评】判定充要条件的基本方法是定义法,即“定条件——找推式——下结论”;有时需要将条件等价转化后再判定.
举一反三:
【变式1】指出下列各题中,![]() 是
是![]() 的什么条件?
的什么条件?
(1) ![]() :
: ![]() ,
, ![]() :
: ![]() ;
;
(2) ![]() :
: ![]() ,
,![]() : 抛物线
: 抛物线![]() 过原点
过原点
(3) ![]() : 一个四边形是矩形,
: 一个四边形是矩形,![]() : 四边形的邻边相等
: 四边形的邻边相等
【答案】
(1)∵![]() :
: ![]() 或
或![]() ,
, ![]() :
: ![]()
∴![]() 且
且![]() ,∴
,∴![]() 是
是![]() 的必要不充分条件;
的必要不充分条件;
(2)∵![]() 且
且![]() ,∴
,∴![]() 是
是![]() 的充要条件;
的充要条件;
(3)∵![]() 且
且![]() ,∴
,∴![]() 是
是![]() 的既不充分条件也不必要条件.
的既不充分条件也不必要条件.
【变式2】判断下列各题中![]() 是
是![]() 的什么条件.
的什么条件.
(1)![]() :
:![]() 且
且![]() ,
, ![]() :
:![]()
(2)![]() :
:![]() ,
, ![]() :
: ![]() .
.
【答案】
(1)![]() 是
是![]() 的充分不必要条件.
的充分不必要条件.
∵![]() 且
且![]() 时,
时,![]() 成立;
成立;
反之,当![]() 时,只要求
时,只要求![]() 、
、![]() 同号即可.
同号即可.
∴必要性不成立.
(2)![]() 是
是![]() 的既不充分也不必要条件
的既不充分也不必要条件
∵![]() 在
在![]() 的条件下才有
的条件下才有![]() 成立.
成立.
∴充分性不成立,同理必要性也不成立.
【变式3】设甲,乙,丙是三个命题,如果甲是乙的充要条件,丙是乙的充分非必要条件,那么丙是甲的( ).
A、充分非必要条件 B、必要非充分条件
C、充要条件 D、既不充分也不必要条件
【答案】A;
【解析】由已知有甲![]() 乙,丙
乙,丙![]() 乙且乙
乙且乙![]() 丙.
丙.
于是有丙![]() 乙
乙![]() 甲,且甲
甲,且甲![]() 丙(否则若甲
丙(否则若甲![]() 丙,而乙
丙,而乙![]() 甲
甲![]() 丙,与乙
丙,与乙![]() 丙矛盾)
丙矛盾)
故丙![]() 甲且甲
甲且甲![]() 丙,所以丙是甲的充分非必要条件.
丙,所以丙是甲的充分非必要条件.
例2.设条件甲为“![]() ”, 条件乙为“
”, 条件乙为“![]() ”那么甲是乙的( )
”那么甲是乙的( )
A、充分不必要条件 B、必要不充分条件
C、充要条件 D、既不充分也不必要条件
【答案】B
【解析】分别解不等式得条件甲为![]() ,乙为
,乙为![]() ,BÜA所以甲是乙的必要不充分条件
,BÜA所以甲是乙的必要不充分条件
【点评】
①先对已知条件进行等价转化化简,然后由定义判断;
②不等式(解集)表示的条件之间的相互关系可以借助集合间的关系判断.
举一反三:
【高清课堂:充分条件与必要条件394804例2】
【变式1】已知p:0<x<3,q:|x-1|<2,则p是q的( )
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分也不必要条件
 【答案】q:|x-1|<2,解得-1<x<3,亦即q:-1<x<3.
【答案】q:|x-1|<2,解得-1<x<3,亦即q:-1<x<3.
如图,在数轴上画出集合P=(0,3),Q=(-1,3),
从图中看PÜQ, p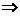 q,但q
q,但q![]() p,所以选择(A).
p,所以选择(A).
【变式2】下列各小题中,![]() 是
是![]() 的什么条件?(在“充分非必要条件”,“必要非充分条件”,“充要条件”“既不充分也不必要条件”中选一种)
的什么条件?(在“充分非必要条件”,“必要非充分条件”,“充要条件”“既不充分也不必要条件”中选一种)
(1) ![]() :
:![]() ,
,![]() :
:![]() 或
或![]() ;
;
(2) ![]() :
:![]() ,
, ![]() :
:![]() 或
或![]() ;
;
(3)![]() :
:![]() ,
,![]() :关于
:关于![]() 的方程
的方程![]() 有实数根.
有实数根.
【答案】(1) ∵![]() ,∴
,∴![]() ,即
,即![]() :
:![]() ,
,
又![]()
![]()
![]()
∴![]() 且
且![]() ,
,
所以![]() 是
是![]() 的充分不必要条件.
的充分不必要条件.
(2) ∵![]() , ∴
, ∴![]() 或
或![]() ,即
,即![]() :
:![]() 或
或![]() ,
,
又![]()
∴![]() 且
且![]() ,即
,即![]()
所以![]() 是
是![]() 的充分必要条件.
的充分必要条件.
(3)∵关于![]() 的方程
的方程![]() 有实数根,
有实数根,
∴ ![]() 即
即![]() ,∴
,∴![]() :
:![]() ,
,
又![]()
![]()
![]()
∴![]() 且
且![]() ,
,
故![]() 是
是![]() 的必要不充分条件.
的必要不充分条件.
【高清课堂:充分条件与必要条件394804例3】
【变式3】设![]() ,则条件“
,则条件“![]() ”的一个必要不充分条件为( )
”的一个必要不充分条件为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
类型二:充要条件的探求与证明
例3. 设x、y∈R,求证:|x+y|=|x|+|y|成立的充要条件是xy≥0.
【解析】
(1)充分性:若xy=0,那么①x=0,y≠0;②x≠0,y=0;③x=0,y=0,
于是|x+y|=|x|+|y|
如果xy>0,即x>0,y>0或x<0,y<0,
当x>0,y>0时,|x+y|=x+y=|x|+|y|.
当x<0,y<0时,|x+y|=-(x+y)=-x+(-y)=|x|+|y|.
总之,当xy≥0时,有|x+y|=|x|+|y|.
(2)必要性:由|x+y|=|x|+|y|及x、y∈R,得(x+y)2=(|x|+|y|)2,
即x2+2xy+y2=x2+2|xy|+y2,|xy|=xy,
∴xy≥0.
综上可得|x+y|=|x|+|y|成立的充要条件是xy≥0.
【点评】充要条件的证明关键是根据定义确定哪是已知条件,哪是结论,然后搞清楚充分性是证明哪一个命题,必要性是证明哪一个命题.
判断命题的充要关系有三种方法:
(1)定义法;
(2)等价法,即利用![]() 与
与![]() ;
;![]() 与
与![]() ;
;![]() 与
与![]() 的等价关系,对于条件或结论是不等关系(否定式)的命题,一般运用等价法.
的等价关系,对于条件或结论是不等关系(否定式)的命题,一般运用等价法.
(3)利用集合间的包含关系判断,若![]() ,则A是B的充分条件或B是A的必要条件;若A=B,则A是B的充要条件.
,则A是B的充分条件或B是A的必要条件;若A=B,则A是B的充要条件.
举一反三:
【变式1】已知a, b, c都是实数,证明ac<0是关于x的方程ax2+bx+c=0有一个正根和一个负根的充要条件.
【答案】
(1)充分性:若ac<0,则Δ=b2-4ac>0,方程ax2+bx+c=0有两个相异实根,设为x1, x2,
∵ac<0, ∴x1·x2=![]() <0,即x1,x2的符号相反,即方程有一个正根和一个负根.
<0,即x1,x2的符号相反,即方程有一个正根和一个负根.
(2)必要性:若方程ax2+bx+c=0有一个正根和一个负根,设为x1,x2,且x1>0, x2<0,
则x1·x2=![]() <0,∴ac<0
<0,∴ac<0
综上可得ac<0是方程ax2+bx+c=0有一个正根和一个负根的充要条件.
【变式2】求关于x的方程ax2+2x+1=0至少有一个负的实根的充要条件.
【答案】
(1)a=0时适合.
(2)当a≠0时,显然方程没有零根,
若方程有两异号的实根,则必须满足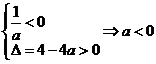 ;
;
若方程有两个负的实根,则必须满足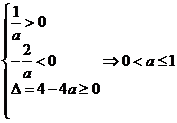
综上知,若方程至少有一个负的实根,则a≤1;
反之,若a≤1,则方程至少有一个负的实根,
因此,关于x的方程ax2+2x+1=0至少有一个负的实根的充要条件是a≤1
类型三:充要条件的应用
例4.已知![]() 若p是q的充分不必要条件,求m的取值范围.
若p是q的充分不必要条件,求m的取值范围.
【答案】![]()
【解析】由![]() 解得
解得![]()
又由![]() 解得
解得![]()
p是q的充分不必要条件,所以
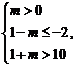 或
或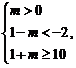
解得![]()
【点评】
解决这类参数的取值范围问题,应尽量运用集合法求解,即先化简集合A、B,再由它们的因果关系,得到A与B的包含关系,进而得到相关不等式组,解之即可.
举一反三:
【变式1】已知命题p:1-c<x<1+c(c>0),命题q:x>7或x<-1,并且p是q的既不充分又不必要条件,则c的取值范围是________.
【答案】0<c≤2
【解析】命题p对应的集合A={x|1-c<x<1+c,c>0},同理,命题q对应的集合B={x|x>7或x<-1}.因为p是q的既不充分又不必要条件,所以![]() 或A不是B的子集且B不是A的子集,所以
或A不是B的子集且B不是A的子集,所以![]() ,①或
,①或![]() ,②,解①得c≤2,解②得c≥-2,又c>0,综上所述得0<c≤2.
,②,解①得c≤2,解②得c≥-2,又c>0,综上所述得0<c≤2.
【变式2】已知p:A={x∈R|x2+ax+1≤0},q:B={x∈R|x2-3x+2≤0},若p是q的充分不必要条件,求实数a的取值范围.
【答案】-2≤a≤2
【解析】B={x∈R|x2-3x+2≤0}={x|1≤x≤2},
∵p是q的充分不必要条件,
∴![]() ,即AÜB,
,即AÜB,
可知![]() 或方程x2+ax+1=0的两根要在区间[1,2]内
或方程x2+ax+1=0的两根要在区间[1,2]内
∴Δ=a2-4<0或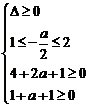 ,得-2≤a≤2.
,得-2≤a≤2.