第三讲 等比数列
教材:等比数列的前![]() 项和
项和
目的:要求学生掌握求等比数列前![]() 项的和的(公式),并了解推导公式所用的方法。
项的和的(公式),并了解推导公式所用的方法。
过程:
一、复习等比数列的通项公式,有关性质,及等比中项等概念。
二、引进课题,采用印度国际象棋发明者的故事,
即求![]() ①
①
用错项相消法推导结果,两边同乘以公比:
![]() ②
②
②-①:![]() 这是一个庞大的数字>1.84×
这是一个庞大的数字>1.84×![]() ,
,
以小麦千粒重为40![]() 计算,则麦粒总质量达7000亿吨——国王是拿不出来的。
计算,则麦粒总质量达7000亿吨——国王是拿不出来的。
三、一般公式推导:设![]() ①
①
乘以公比![]() ,
,![]() ②
②
①-②:![]() ,
,![]() 时:
时:![]()
![]() 时:
时:![]()
注意:(1)![]() 和
和![]() 各已知三个可求第四个,
各已知三个可求第四个,
(2)注意求和公式中是![]() ,通项公式中是
,通项公式中是![]() 不要混淆,
不要混淆,
(3)应用求和公式时![]() ,必要时应讨论
,必要时应讨论![]() 的情况。
的情况。
四、例1、(P131,例一略)——直接应用公式。
例2、(P131,例二略)——应用题,且是公式逆用(求![]() ),要用对数算。
),要用对数算。
例3、(P131-132,例三略)——简单的“分项法”。
例4、设数列![]() 为
为![]()
![]() 求此数列前
求此数列前![]() 项的和。
项的和。
解:(用错项相消法) ![]() ①
①
![]() ②
②
①-②![]() ,
,
当![]() 时,
时,
![]()
![]()
当![]() 时,
时,![]()
五、小结:(1)等比数列前![]() 项和的公式,及其注意点,(2)错项相消法。
项和的公式,及其注意点,(2)错项相消法。
再介绍两种推导等比数列求和公式的方法,(作机动)
法1:设![]()
∵![]() 成GP,∴
成GP,∴![]()
由等比定理:![]() 即:
即:![]()
当![]() 时,
时,![]()
当![]() 时,
时,![]()
法2:![]()
![]()
![]()
从而:![]() 当
当![]() 时
时![]() (下略)
(下略)
当![]() 时
时![]()
六、作业:P132-133 练习 ①,②,③
习题3.5 ①,②,③,④,⑤
第四讲 等比数列
教材:等比数列综合练习
目的:系统复习等比数列的概念及有关![]() 知识,要求学生能熟练的处理有关问题。
知识,要求学生能熟练的处理有关问题。
过程:
一、处理《教学与测试》P8![]() 7第42课习
7第42课习![]() 题课(2)
题课(2)
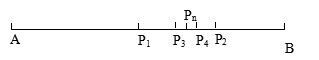 1、“练习题”1 选择题。
1、“练习题”1 选择题。
2、(例一)略:注意需用性质。![]()
3、(例三)略:作图解决:
解:![]()
![]()
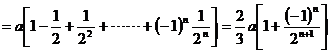
二、![]() 补充例题:
补充例题:
1、在等比数列![]() 中,
中,![]() ,求
,求![]() 的范围。
的范围。
解:∵![]() ,∴
,∴![]()
又∵![]() ,且
,且![]() ,∴
,∴![]() ,
,
∴![]() 解之:
解之: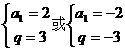
当![]() 时,
时,![]() ,∴
,∴![]()
(∵![]()
![]() )
)
当![]() 时,
时,![]() ,
,
∵![]() 且必须为偶数
且必须为偶数
∴![]() ,(∵
,(∵![]() )
)
2、等比数列![]() 前
前![]() 项和
项和![]() 与积分别为S和T,数列
与积分别为S和T,数列![]() 的前
的前![]() 项和
项和![]() 为
为![]() ,
,
求证: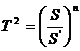
证:当![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,
∴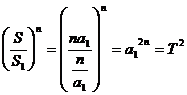 ,(成立)
,(成立)
当![]() 时,
时,![]() ,
,
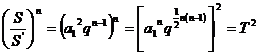 ,(成
,(成![]() 立)
立)
综上所述:命题成立。
3、设首项为正数的等比数列,它的前![]() 项之和为80,前
项之和为80,前![]() 项之和为6560,且前
项之和为6560,且前
![]() 项中数值****的项为54,求此数列。
项中数值****的项为54,求此数列。
解:
![]() 代入(1),
代入(1), ![]() ,得:
,得:![]() ,从而
,从而![]() ,
,
∴![]() 递增,∴前
递增,∴前![]() 项中数值****的项应为第
项中数值****的项应为第![]() 项。
项。
∴![]() ,∴
,∴![]() ,
,
∴![]() ,∴此数列为
,∴此数列为![]()
4、设数列![]() 前
前![]() 项之和为
项之和为![]() ,若
,若![]() 且
且![]() ,
,
问:数列![]() 成GP吗?
成GP吗?
解:∵![]() ,∴
,∴![]() ,即
,即![]()
即:![]()
![]() ,∴
,∴![]() 成GP
成GP![]()
又:![]() ,
,
∴![]() 不成GP,但
不成GP,但![]() 时
时![]() 成GP,即:
成GP,即:![]() 。
。
三、作业![]() :《教学与测试》P87-88 练习题 3,4,5,6,7
:《教学与测试》P87-88 练习题 3,4,5,6,7
补充:1、三数成GP,若将第三数减去32,则成AP,若将该等差数列中项减
![]() 去4,以成GP,求原三数。(2,10,50或
去4,以成GP,求原三数。(2,10,50或![]() )
)
2![]() 、一个等比数列前
、一个等比数列前![]() 项的和为
项的和为![]() 前
前![]() 项之和
项之和![]()
![]() ,求
,求![]() 。
。
(63)
![]() 3、在等比数列中,已知:
3、在等比数列中,已知:![]() ,求
,求![]() 。
。 ![]()
《精编》P176-177 第2,4题。