第三教时

教材：等差数列（一）

目的：要求学生掌握等差数列的意义，通项公式及等差中项的有关概念、计算公式，并能用来解决有关问题。

过程：

一、 引导观察数列：4，5，6，7，8，9，10，…… 

                                                 3，0，-3，-6，……

                                        ，，，，……

                        12，9，6，3，……

       特点：从第二项起，每一项与它的前一项的差是常数 — “等差”

二、 得出等差数列的定义： （见P115）

        注意：从第二项起，后一项减去前一项的差等于同一个常数。

1．名称：AP     首项   公差 

2．若  则该数列为常数列

3．寻求等差数列的通项公式： 

               

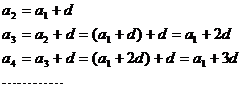
    由此归纳为     当时  （成立）

       注意:  1° 等差数列的通项公式是关于的一次函数

              2° 如果通项公式是关于的一次函数，则该数列成AP

          证明：若

                它是以为首项，为公差的AP。

              3° 公式中若  则数列递增， 则数列递减

  4° 图象： 一条直线上的一群孤立点

三、例题： 注意在中，，，四数中已知三个可以求    

       出另一个。

例一 （P115例一）

例二 （P116例二）  注意：该题用方程组求参数

例三 （P116例三）  此题可以看成应用题

四、 关于等差中项： 如果成AP 则

      证明：设公差为，则  

            ∴

   例四  《教学与测试》P77 例一：在-1与7之间顺次插入三个数使这五个数成AP，求此数列。

       解一：∵  ∴是-1与7 的等差中项

             ∴   又是-1与3的等差中项  ∴

             又是1与7的等差中项  ∴

       解二：设 ∴ 

             ∴所求的数列为-1，1，3，5，7

五、小结：等差数列的定义、通项公式、等差中项

六、作业： P118 习题3．2    1-9