函数的表示法

（一） 映射的概念教学：

定义：

一般地，设A、B是两个非空的集合，如果按某一个确定的对应法则f，使对于集合A中的任意一个元素x，在集合B中都有****确定的元素y与之对应，那么就称对应为从集合A到集合B的一个映射（mapping）。记作：

讨论：映射有哪些对应情况？一对多是映射吗？

例1．以下给出的对应是不是从A到集合B的映射？

（1） 集合A={P | P是数轴上的点}，集合B=R，对应关系f：数轴上的点与它所代表的实数对应；

（2） 集合A={P | P是平面直角坐标系中的点}，B= ，对应关系f： 平面直角坐标系中的点与它的坐标对应；

（3） 集合A={x | x是三角形}，集合B={x | x是圆}，对应关系f：每一个三角形都对应它的内切圆；

（4） 集合A={x | x是新华中学的班级}，集合B={x | x是新华中学的学生}，对应关系：每一个班级都对应班里的学生。

例1、判断下列对应是否映射？有没有对应法则？

   

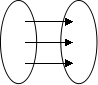
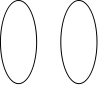
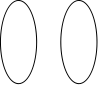
        a        e        a       e        a        e

        b        f        b       f        b        f

        c        g        c       g       c         g

                          d                        d

例2、下列对应是不是从A到B的映射？

（1）

（2）

（3）

（4）A=

(5) 设A={矩形}，B={实数}。对应法则f为矩形到它的面积的对应;

(6) 设A={实数}，B={正实数}。对应法则f为。

例3．设集合A={a,b,c}，B={0,1} ，试问：从A到B的映射一共有几个？并将它们分别表示出来。

例4、 设是从A到B的一个映射,其中.

则A中的元素(-1,2)的象是        ,

B中的元素(-1,2)的原象是             .

针对训练：         

1．关于从集合A到集合B的映射，下列说法错误的是（  ）

A．A中每个元素在B中都有象      B．A中的两个不同元素在B中的象必不同

C．B中的元素在A中可以没有原象  D．B中的元素在A中的原象可能不止一个

2．已知映射：，其中，集合B中的元素都是A中的元素在映射f下的象，且对任意的，在B中和它对应的元素是，则集合B中元素的个数是（  ）

A．4           B. 5         C.6        D.7

3．若A=,定义从A到B的一个映射

4．在，，且

则A中的元素(-1,2)的象是        ,B中的元素(-1,2)的原象是       .

5．映射为，映射为，

则：映射是                    

求函数的解析式：

常见的求函数解析式的方法有待定系数法，换元法，配凑法，消去法。

例5．已知f(x)是一次函数，且满足3f(x+1)-2f(x-1)=2x+17，求函数f(x)的解析式。

      （待定系数法）

例6．已知f(2x+1)=3x-2，求函数f(x)的解析式。（配凑法或换元法）

例7．已知函数f(x)满足，求函数f(x)的解析式。（消去法）

课堂练习：

   1．已知 ，求函数f(x)的解析式。    

2．已知，求函数f(x)的解析式。

3．已知，求函数f(x)的解析式。

4.设，则是                                        （    ）

A.           B.          C.         D.