函数的表示法

复习准备：

1．举例初中已经学习过的一些函数的图象，如一次函数，二次函数，反比例函数的图象，

2. 回忆：函数图象有什么特点？

讲授新课：

例1、某种笔记本每个5元，买（ x{1,2,3,4}）个笔记本的钱数记为y（元），试写出以x为自变量的函数y的解析式，并画出这个函数的图像

例2．画出下列各函数的图象，求下列函数的值域：

（1）

（2）   ① ；   ② ；     ③ .

（3）  ① ；   ②

（4）；

（5）  ①时，        ；

②时，        ；

③时，        。

例3．画出函数的图象。

例4.画图求值域：  

例5．设，求函数的解析式，并画出它的图象。

变式1：求函数的****值。

变式2：解不等式。

例6．当m为何值时，方程有4个互不相等的实数根。

例7．画出函数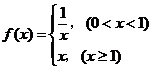的图象。

函数及其表示复习课

基础习题练习：（口答下列基础题的主要解答过程 → 指出题型解答方法）

1．说出下列函数的定义域与值域： ； ；  ；

2．已知，求， ， ；

典型例题：

例１．已知函数=4x+3，g(x)=x,　求f[f(x)]，f[g(x)]，g[f(x)]，g[g(x)]．

例2．求下列函数的定义域：

　（１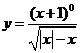）；　　　　　　　　（２）；

例４． 中山移动公司开展了两种通讯业务：“全球通”，月租50元，每通话1分钟，付费0.4元；“神州行”不缴月租，每通话1分钟，付费0.6元. 若一个月内通话x分钟，两种通讯方式的费用分别为（元）．

（１）．写出与x之间的函数关系式？  

（２）．一个月内通话多少分钟，两种通讯方式的费用相同？ 

（３）．若某人预计一个月内使用话费200元，应选择哪种通讯方式？

课下作业：

1．已知=x-x+3 ，求：f(x+1)， f()的值；

2．若,求函数的解析式；