考向二 函数的解析式
1.【2018届山东省滕州市第三中学高三】一次函数g(x)满足g[g(x)]=9x+8,则g(x)是( )
A. g(x)=9x+8 B. g(x)=3x+8
C. g(x)=﹣3x﹣4 D. g(x)=3x+2或g(x)=﹣3x﹣4
【答案】D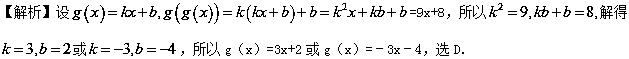
2.【2018届河北省大名县第一中学高三上学期第一次月考】下列各组函数中,表示同一函数的是( )
A.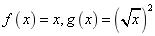 B.
B. 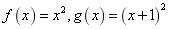
C. 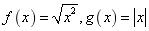 D.
D. 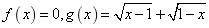
【答案】C
【解析】∵f(x)=x (x∈R)与 ![]() (x⩾0)两个函数的定义域不一致,
(x⩾0)两个函数的定义域不一致,
∴A中两个函数不表示同一函数;
∵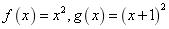 两个函数的对应法则不一致,
两个函数的对应法则不一致,
∴B中两个函数不表示同一函数;
∵ ,且两个函数的定义域均为R
,且两个函数的定义域均为R
∴C中两个函数表示同一函数;
f(x)=0,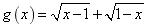 (x=1)两个函数的定义域不一致,
(x=1)两个函数的定义域不一致,
∴D中两个函数不表示同一函数;
故选C.
3.数列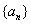 是递增数列,且满足
是递增数列,且满足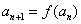 ,
,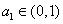 ,则f(x)不可能是( )
,则f(x)不可能是( )
A.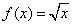 B.
B.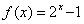 C.
C.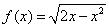 D.
D.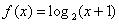
【答案】B.
【解析】

4.已知函数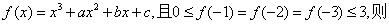 ( )
( )
A.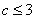 B.
B. 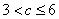 C.
C. 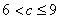 D. c>9
D. c>9
【答案】C
【解析】由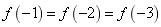 得,
得,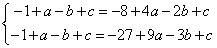 ,解得
,解得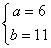 ,所以
,所以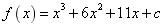 ,由
,由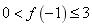 ,得
,得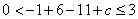 ,即
,即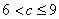 ,故选C.
,故选C.
【解题技巧】(1)配凑法:由已知条件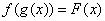 ,可将f(x)改写成关于g(x)的表达式,然后以x替代g(x),便得f(x)的解析式;
,可将f(x)改写成关于g(x)的表达式,然后以x替代g(x),便得f(x)的解析式;
(2)待定系数法:若已知函数的类型(如一次函数、二次函数),可用待定系数法;
(3)换元法:已知复合函数f(g(x))的解析式,可用换元法,此时要注意新元的取值范围;
(4)方程思想:已知关于f(x)与![]() 或f(-x)的表达式,可根据已知条件再构造出另外一个等式组成方程组,通过解方程组求出f(x).
或f(-x)的表达式,可根据已知条件再构造出另外一个等式组成方程组,通过解方程组求出f(x).
【易错点睛】解决函数解析式问题,必须优先考虑函数的定义域,用换元法解题时,应注意换元前后的等价性.