专题4      三角函数

一、知识归纳：

二、自我小测：

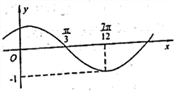1、函数f（x）＝sin（）（其中）的图象如图所求，为了得到g（x）＝sin的图象，可以将f（x）的图象

（A）右移（B）右移（C）左移（D）左移

2、如果若干个函数图象经过平移后能够重合，则称这些函数为“同簇函数”.

①； ②；

③；  ④.其中“同簇函数”的是(    )

A．①②      B．①④        C．②③             D．③④ 

3、已知船在灯塔北偏东处，且船到灯塔的距离为2km，船在灯塔北偏西处，、两船间的距离为3km，则B船到灯塔的距离为__________km。

4、E，F是等腰直角△ABC斜边AB上的三等分点，则

  A．       B．      C．      D． 

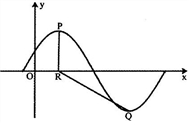5、已知f(x)＝Asin()(A>0，0<<)的部分图象如图所示，P、Q分别为该图象的****点和最低点，点P的坐标为(2，A)，点R的坐标为(2，0)。若∠PRQ＝，则y＝f(x) 的****值及的值分别是

A.2,　 B.,　C.,　D. 2,　

三、经典例题：

l 取值范围问题：

1、已知，满足． 

（I）将表示为的函数，并求的最小正周期；

（II）若，且，求的取值范围．

2、已知锐角中内角、、的对边分别为、、，，且.

（Ⅰ）求角的值；

（Ⅱ）设函数，图象上相邻两****点间的距离为，求的取值范围.

3、已知向量，,且.

(Ⅰ)求角的大小;(Ⅱ)若向量,试求的取值范围.

4、已知函数（），直线，是图象的任意两条对称轴，且的最小值为．

（I）求的表达式；

（Ⅱ）将函数的图象向右平移个单位后，再将得到的图象上各点的横坐标伸长为原来的2倍，纵坐标不变，得到函数的图象，若关于的方程，在区间上有且只有一个实数解，求实数的取值范围.

l 面积问题：

1、已知向量且m//n.

   （I）求角A的大小；   （II）若面积的****值。

2、已知函数

    (I)求函数的最小正周期及在区间上的值域；

(Ⅱ)在ABC中，角A、B、C所对的边分别是a、b、c，又的面积等于3，求边长a的值．

3、已知向量，设函数,若函数的图象与的图象关于坐标原点对称.

（Ⅰ）求函数在区间上的****值,并求出此时的值；

（Ⅱ）为锐角,若，，的面积为，求边的长．

l 实际应用问题：

1、在某海岸A处，发现北偏东方向，距离A处n mile的B处有一艘走私船在A处北偏西的方向，距离A处n mile的C处的缉私船奉命以n mile/h的速度追截走私船. 此时，走私船正以5 n mile/h的速度从B处按照北偏东方向逃窜，问缉私船至少经过多长时间可以追上走私船，并指出缉私船航行方向.   

2、某城市有一块不规则的绿地如图所示，城建部门欲在该地上建造一个底座为三角形的环境标志，小李、小王设计的底座形状分别为△ABC、△ABD，经测量AD=BD=14，BC=10,AC=16,∠C=∠D．

(I)求AB的长度；

(Ⅱ)若建造环境标志的费用与用地面积成正比，不考虑其他因素，小李、小王谁的设计使建造费用最低，请说明理由．

四、课后作业：

1、设函数，则下列结论正确的是

A．把的图象向左平移个单位，得到一个偶函数的图象

B．的图象关于点对称

C．的最小正周期为，且在上为增函数

D．f（x）的图象关于直线x＝对称

2、已知函数的****值为4，最小值为0，两条对称轴间的最短距离为,直线是其图象的一条对称轴，则符合条件的解析式是(    )

A.      B．

 C.   D．

3、为了得到函数的图象，只需将函数的图象

A.向左平移个长度单位 B.向右平移个长度单位

C.向左平移个长度单位     D.向右平移个长度单位

4、已知函数，且函数的最小正周期为。（Ⅰ）求函数的解析式；（Ⅱ）在中，角A，B，C所对的边分别为，若，且，试求的值。

版权所有：高考资源网(www.k s 5 u.com)