专题六     立体几何

一、知识归纳：

二、自主小测：

1、某几何体的三视图如图所示,则该几何体的体积为

（　　）

A． B． C． D．

【答案】A 

2、已知三棱柱的侧棱与底面垂直,体积为,底面是边长为的正三角形.若为底面的中心,则与平面所成角的大小为 （　　）

A． B． C． D．    【答案】B 

3、已知三棱柱的6个顶点都在球的球面上,若,,,则球的半径为 （　　）

A． B． C． D． 【答案】C 

4、已知圆和圆是球的大圆和小圆,其公共弦长等于球的半径,,且圆与圆所在的平面所成的一个二面角为,则球的表面积等于______.  【答案】 

三、经典例题：

l 证明平行、垂直问题：

例：如图,在三棱锥中,平面平面,,,过作,垂足为,点分别是棱的中点.

求证:(1)平面平面;  (2).

       

l 线面角问题：

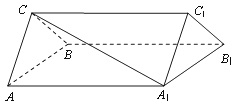
例：如图,三棱柱ABC-A1B1C1中,CA=CB,AB=A A1,∠BA A1=60°.

(Ⅰ)证明AB⊥A1C;

(Ⅱ)若平面ABC⊥平面AA1B1B,AB=CB=2,求直线A1C 与平面BB1C1C所成角的正弦值.

l 求距离问题：

例：如图,在长方体ABCD-A1B1C1D1中,AB=2,AD=1,A1A=1,证明直线BC1平行于平面DA1C,并求直线BC1到平面D1AC的距离.

l 求体积问题：

例：如图,在正三棱锥中,,异面直线与所成角的大小为,求该三棱柱的体积. 

l 求二面角问题：

例1、如图,AB是圆的直径,PA垂直圆所在的平面,C是圆上的点.

(I)求证:

(II)

 

例2、如图,四棱锥中,,

,

为的中点,.

(1)求的长;     (2)求二面角的正弦值.

例3、如图,在四面体中,平面,.

是的中点, 是的中点,点在线段上,且.

(1)证明:平面;(2)若二面角的大小为,求的大小.

例4、如图,在直三棱柱中,,,,点是的中点

(1)求异面直线与所成角的余弦值

(2)求平面与所成二面角的正弦值.

                                    

例5、直棱柱中,分别是的中点,.

(Ⅰ)证明:平面;   (Ⅱ)求二面角的正弦值.

l 折叠问题：

例：如图1,在等腰直角三角形中,,,分别是上的点,,为的中点.将沿折起,得到如图2所示的四棱锥,其中.

(Ⅰ) 证明:平面;      (Ⅱ) 求二面角的平面角的余弦值.

l 动点问题：

例1、如图, 四棱柱ABCD-A1B1C1D1中, 侧棱A1A⊥底面ABCD, AB//DC, AB⊥AD, AD = CD = 1, AA1 = AB = 2, E为棱AA1的中点. 

(Ⅰ) 证明B1C1⊥CE; 

(Ⅱ) 求二面角B1-CE-C1的正弦值. 

(Ⅲ) 设点M在线段C1E上, 且直线AM与平面ADD1A1所成角的正弦值为, 求线段AM的长. , ;

例2、如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.

(Ⅰ)求证:AA1⊥平面ABC;

(Ⅱ)求二面角A1-BC1-B1的余弦值;

(Ⅲ)证明: 在线段BC1存在点D,使得AD⊥A1B,并求的值.